Потеря устойчивости основные понятия
В инженерной практике
- Устойчивость – это способность конструкции сохранять свое первоначальное положение или форму.
- Потерей устойчивости - переход конструкции из устойчивого состояния в неустойчивое.
- Критическое состояние - граница перехода из одного состояния в другое.
- Критическая нагрузка - нагрузка, при действии которой конструкция переходит в критическое состояние.

Различают два рода потери устойчивости:
Потеря устойчивости первого рода связана с появлением нового вида деформации и характеризуется нарушением равновесия между нагрузкой и внутренними усилиями и свойственна только упругим системам.
Потеря устойчивости второго рода наблюдается при потере несущей способности всей конструкции и характеризуется резким, неконтролируемым возрастанием предыдущих деформаций. В этом случае равновесие между нагрузкой и внутренними усилиями нарушается даже без появления новых видов деформаций.
Математически потеря устойчивости является задачей о бифуркации.
Точка бифуркации — критическое состояние конструкции, при котором она становится неустойчивой относительно незначительного отклонения действующих нагрузок или геометрической формы конструкции.
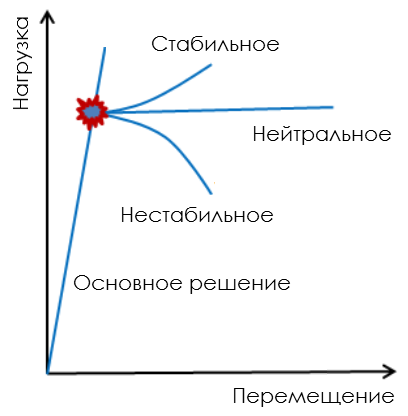
При определенном уровне нагрузки существует более одного решения. На диаграмме показана точка бифуркации и три возможных решения, исходящих из нее.
Если нагрузка продолжает возрастать, то решение можно отнести к стабильным. Это наименее опасная ситуация, но если вы ее не распознаете, то в результате вычислений, скорее всего, получите слишком малые напряжения. Это приведет к недооценке критической нагрузки. Нейтральное и нестабильное решение являются более опасными, поскольку при критической нагрузке ограничения на перемещения отсутствуют.
При наличии более одного решения возникает вопрос, какое из них является корректным. Все решения удовлетворяют уравнениям равновесия, но в реальном мире поведение структуры будет соответствовать одной определенной траектории. Будет реализована та траектория, которая позволяет минимизировать энергию.
Потеря устойчивости в линейной постановке задачи
Отличие линейного статического анализа от анализа на потерю устойчивости заключаются в следующем:
При линейном статическом анализе конструкции имеют место следующие условия:
- форма деформирования конструкции под нагрузкой является единственной и не изменяется при пропорциональном изменении компонент вектора нагрузки;
- после того, как нагрузка будет снята, конструкция возвращается в исходное состояние.
Условия для анализа конструкции на потерю устойчивости:
- форма деформирования конструкции под нагрузкой может отличаться по направлению перемещений точек конструкции по отношению к действующей нагрузке, когда значение нагрузки достигнет критического значения.
Явление потери устойчивости конструкции в линейной постановке (Buckling) рассматривается при следующих допущениях о предполагаемом поведении конструкции:
- используется линейный материал;
- перемещения малы и направление нагрузки не изменяется в процессе деформирования конструкции.
Если одно из перечисленных выше условий не выполняется, линейный анализ не может считаться достоверным. В этом случае требуется выполнять нелинейный деформационный анализ конструкции (Nonlinear Static), строить диаграмму равновесных состояний, и по её виду судить об устойчивости конструктивных элементов или конструкции в целом.
Потеря устойчивости в линейной постановке
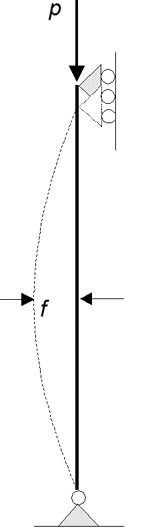
Решением задачи линейной статики является единственное положение равновесия деформированной конструкции и относящиеся к нему внутренние усилия. Однако в линейном статическом расчете не обосновывается устойчивость полученного положения равновесия. Если подвергать осевому сжатию тонкую металлическую линейку, то при некотором значении сжимающей силы прямолинейная форма равновесия линейки становится неустойчивой, происходит ее выпучивание. Этот пример показывает, что при определенных условиях возможно не единственное положение равновесия – в данном случае их два: прямолинейное и искривленное.
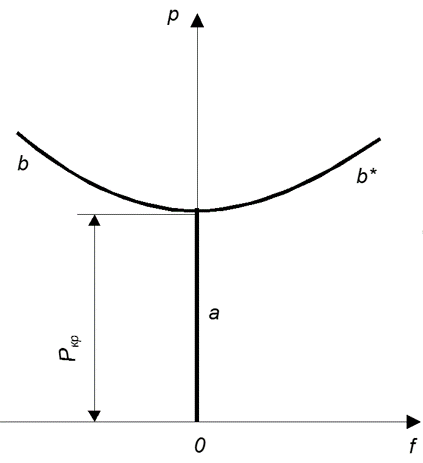
Состояние равновесия упругой системы можно определить двумя параметрами: характерным перемещением f и параметром нагрузки p.
Возможным состояниям равновесия соответствует диаграмма равновесных состояний: кривая в системе осей p – f .
При любом значении p<pкр существует единственное и устойчивое состояние равновесия, которое определяет прямая a.
При p≥pкр есть несколько состояний равновесия – две устойчивые формы: кривые b и b* , и исходная форма a, которая становится неустойчивой.
При потере устойчивости конструкция переходит из одной устойчивой формы сжатого стержня, в другую устойчивую форму изогнутой балки.
Выражение для определения критической нагрузки консольно закрепленного стержня
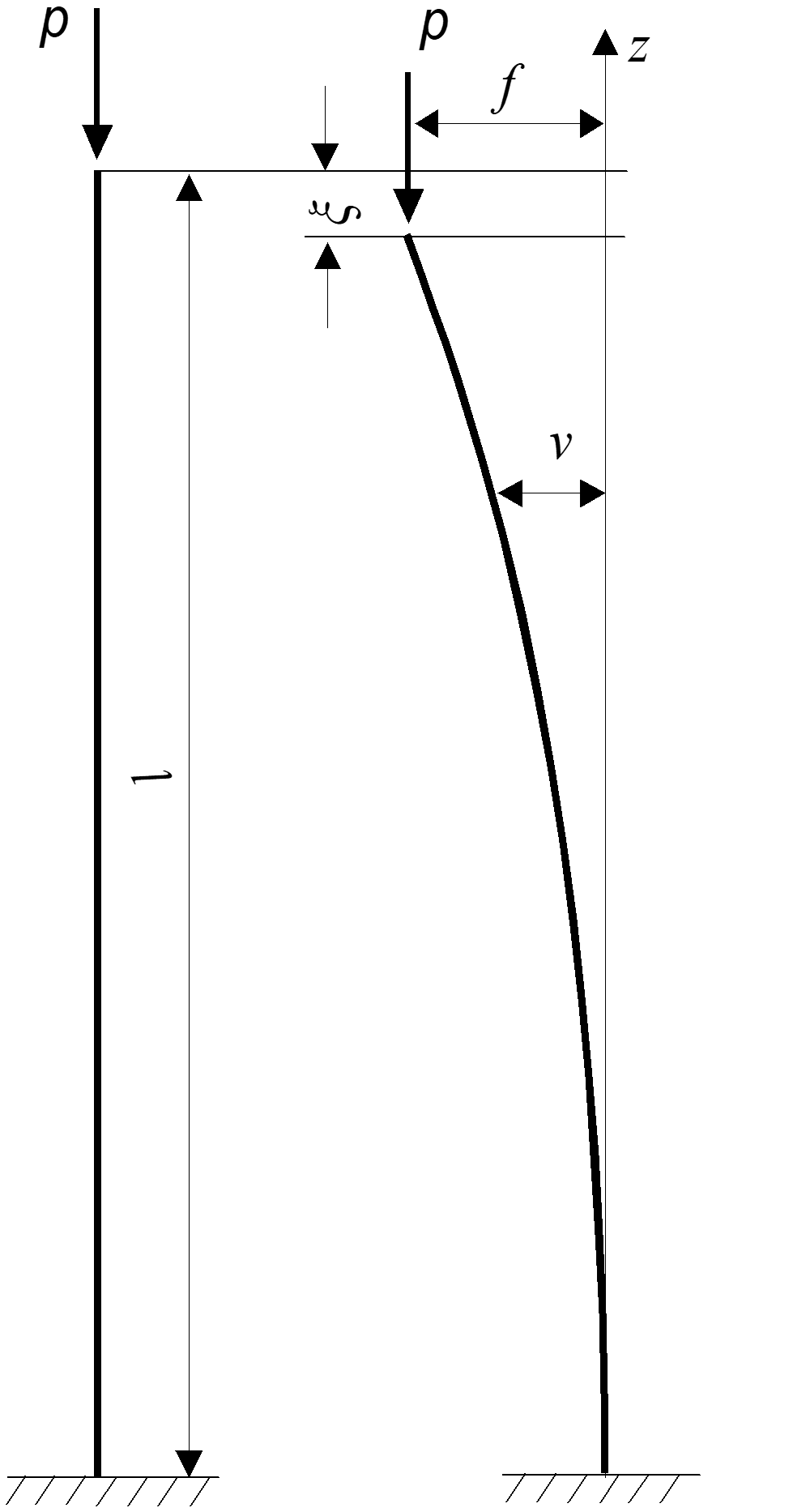
Предположим, что при действии осевой сжимающей силы произошло некоторое боковое смещение f <<l конца стержня, тогда энергия деформации увеличится на величину энергии изгиба стержня ΔU.
Одновременно, потенциальная энергия нагрузки уменьшится из-за понижения на величину ξ точки её приложения.
Уменьшение потенциальной энергии равно работе ΔW, произведенной нагрузкой в результате понижения точки приложения силы.
Прямая форма сжатого стержня будет устойчивой, если ΔU–ΔW>0 и неустойчивой, если ΔU–ΔW<0.
Критическое значение нагрузки, при котором конструкция из прямолинейной формы равновесия переходит в криволинейную форму, определяется из уравнения ΔU=ΔW.
Форма изогнутой оси стержня описывается функцией:
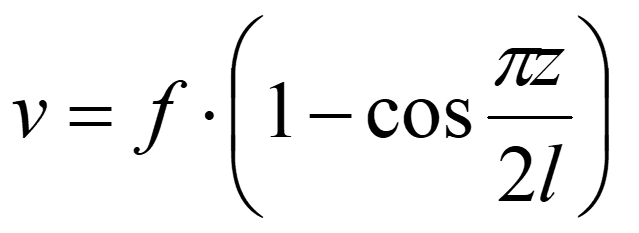
Изгибающий момент в произвольном сечении z:
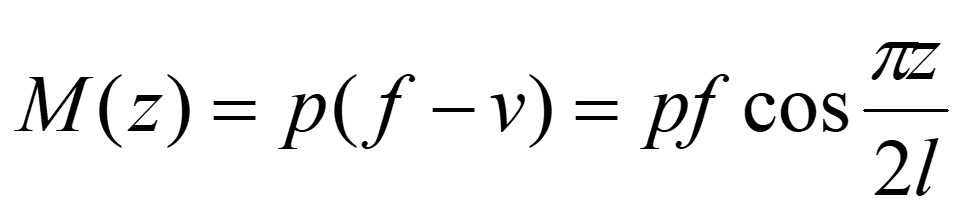
Энергия изгиба стержня равна:
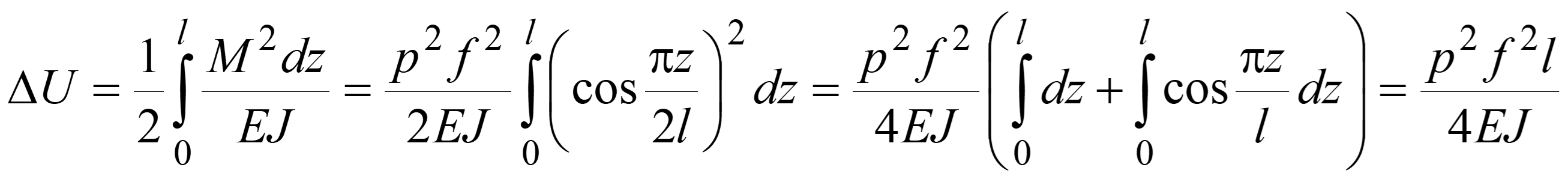
Поскольку принято, что f<<l, то смещение участка стойки dξ в вертикальном направлении равно:
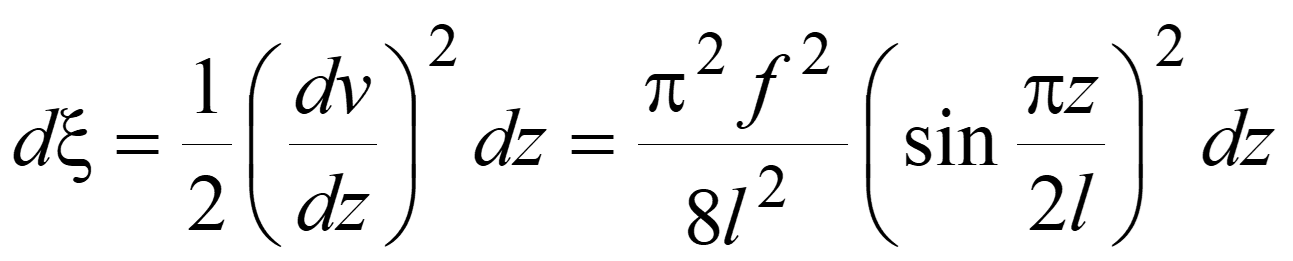
Отсюда полное вертикальное смещение верхнего конца стойки:

Теория анализа на потерю устойчивости методом конечных элементов
Решим поставленную задачу методом конечных элементов, аппроксимируя прогиб через смещения узлов и углы поворота линии прогиба в узлах элементов.


Для определения критических значений нагрузки используется энергетический метод, суть которого состоит в отслеживании изменения полной потенциальной энергии системы при переходе из одной формы равновесия в другую. При этом точке бифуркации соответствует нулевое значение изменения общей потенциальной энергии.

Как правило, среди полученных критических значений нагрузки большое значение имеет только первое, так как в большинстве случаев происходит разрушение конструкции до достижения следующего критического значения
Таким образом линейный анализ устойчивости методом конечных элементов разбивается на два следующих этапа:
- На первом этапе решается задача линейной статики для конструкции, нагруженной единичным вектором {R0}. Определяется статическая форма равновесия и соответствующее ей распределение внутренних сил в элементах.
- На втором этапе вычисляется геометрическая матрица жесткости конструкции, соответствующая этим внутренним усилиям, и затем вычисляется один или несколько корней уравнения для условия равновесия системы и соответствующих им форм потери устойчивости. Задача вычисления этих корней уравнения называется проблемой собственных значений.
Расчет потери устойчивости цилиндрической оболочки
Рассмотрим классическую задачу потери устойчивости цилиндрической оболочки при осевом сжатии.
Параметры оболочки:
- высота цилиндра: 50 см;
- радиус цилиндра: 20 см;
- толщина стенки: 0.1 см;
- параметры изотропного материала: E=21000 кН/см2, μ=0.3.

Создаем поверхность оболочки методом «вытягивания» окружности
Меню Geometry->Surface->Extrude
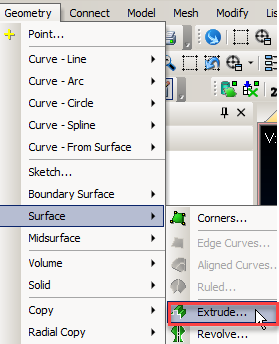
Далее выбираем кривую (Curve) построенной окружности

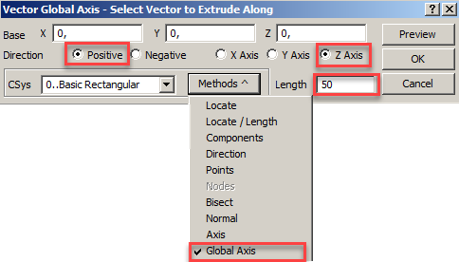
Затем в окне выбора направления вытягивания выбираем Methods->Global Axis;
Direction->Positive Z Axis; Length->50
Создаем материал и свойства для элементов
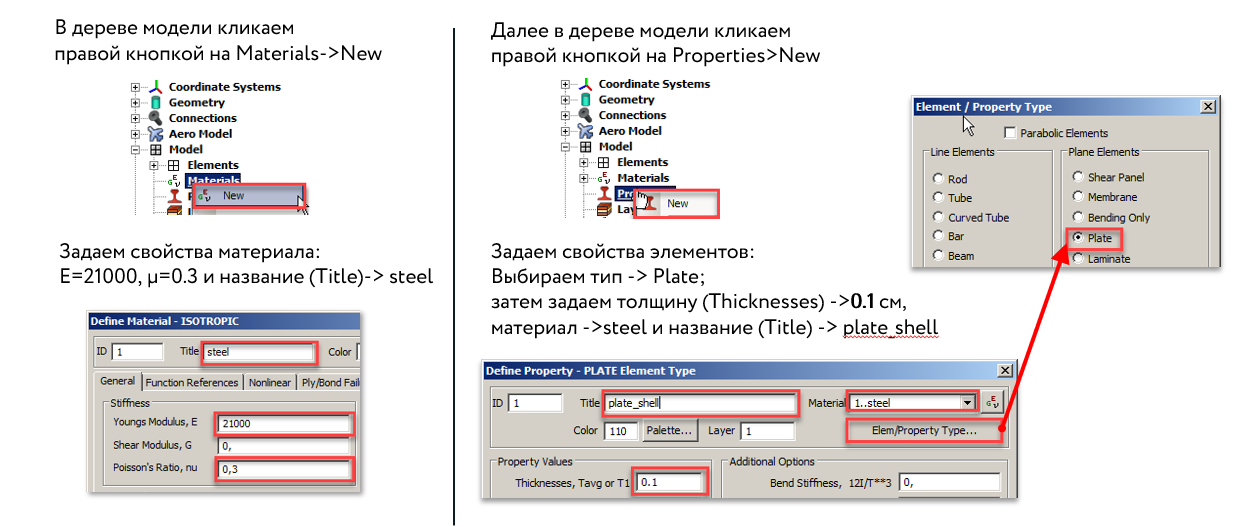

Создаем элементы RBE2
На панели инструментов Custom Tool выбираем меню Meshing->Spider Nodes
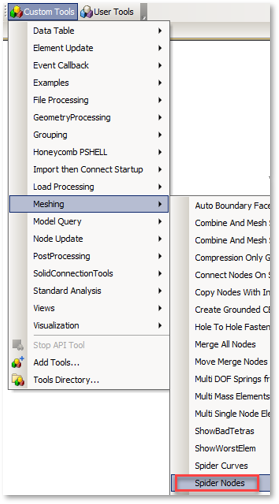
Выбираем метод привязки при выборе «on Curve» и выбираем верхние дуги окружности.
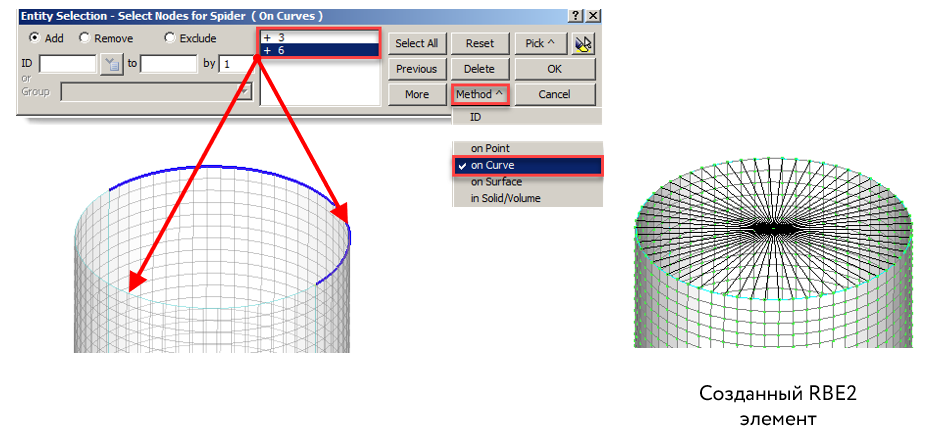
Повторяем данную операцию для нижнего торца оболочки
Создаем закрепление и нагрузку
В меню выбираем Model->Loads->Nodal
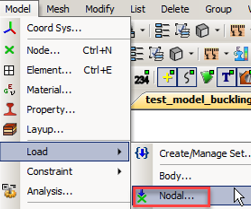
Выбираем центральный узел RBE2 элемента, находящегося вверху оболочки и нажимаем ОК

В открывшемся окне, задаем начальное осевое усилие FZ=-10000 кН и название (Title) нагрузки «Buckling_load»
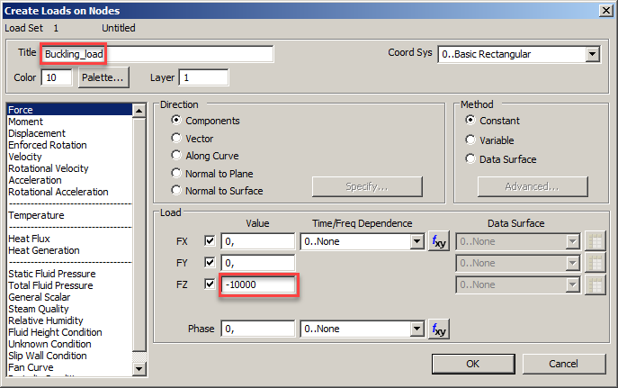
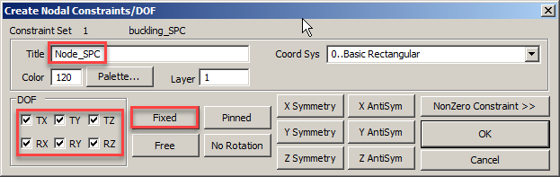
Создаем закрепление и нагрузку. В меню выбираем Model->Constrain->Nodal
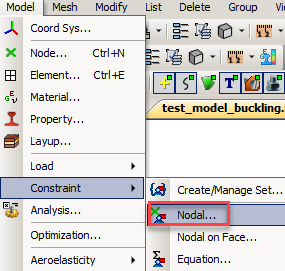
Создаем новый «набор» закреплений с названием (Title) «Buckling_SPC»
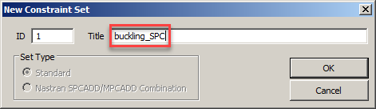
Выбираем центральный узел RBE2 элемента, построенного внизу оболочки и нажимаем ОК
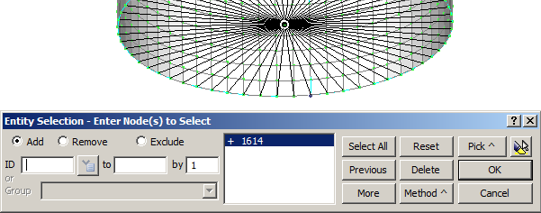
В открывшемся окне, задаем закрепление по всем степеням свободы нажав кнопку Fixed, вводим название (Title) закрепления «Node_SPC»
Настраиваем параметры расчета
В дереве модели кликаем правой кнопкой на Analyses->Manage
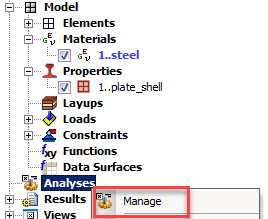
В окне Analysis Set Manager нажимаем кнопку New;
В окне Analysis Set выбираем тип решения (Analysis Type) –> Buckling
Далее кликаем кнопку Next до появления окна NASTRAN Buckling Analysis
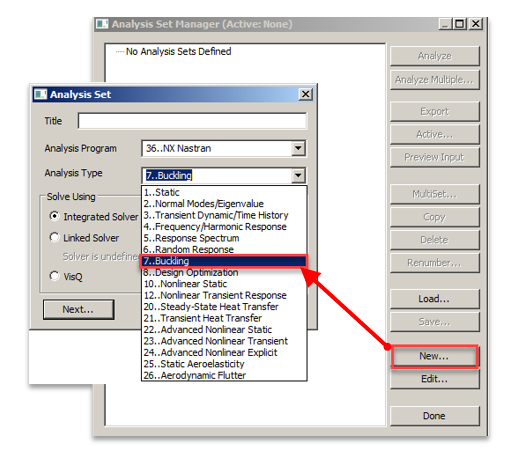
Настраиваем параметры расчета
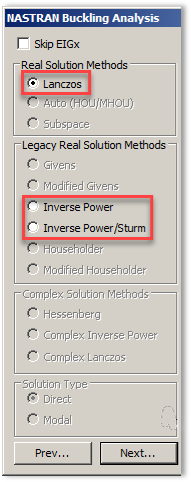
В решателе NX Nastran линейный анализ устойчивости выполняется с использованием решения SEBUCKL 105.
Для поиска собственных значений при решении линейных задач устойчивости может быть использован один из трех методов:
- Метод Ланцоша, используемый по умолчанию, современный эффективный метод сочетающий в себе лучшее из ранее применяемых методов для получения собственных значений с высокой точностью. Метод поддерживает распараллеливание по процессорам.
Классические методы:
- Метод обратных итераций заключается в выделении нижних собственных значений и векторов в желаемом диапазоне. Затем их влияние исключается и вычисляется следующее, высшее, значение с повторением процедуры исключения. Каждое из собственных значении находится с помощью итерационной процедуры. К сожалению, в зависимости от определения диапазона поиска собственных значений, может пропускать некоторые моды, что делает его недостаточно надежным.
- Метод обратных итераций с использованием процедуры последовательности Штурма для проверки того, что в выбранном диапазоне обнаружены все собственные значения. При его использовании выдается сообщение о числе собственных значений ниже выбранного пробного значения.
Настраиваем параметры расчета
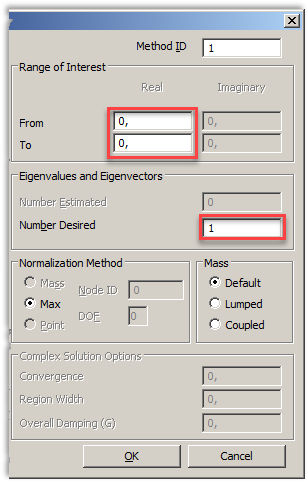
В правой части окна NASTRAN Buckling Analysis пользователь также может задать:
- Диапазон для поиска критический значений lкр для приложенной нагрузки
- Количество критических значений (возможных корней уравнения).
Напомним, что среди полученных критических значений наиболее важным является только первое, так как в большинстве случаев происходит разрушение конструкции до достижения следующего критического значения. То есть поиск дополнительных критических значений для инженерной практики существенного смысла не имеет.
В любом случае в результате решения SEBUCKL 105 пользователю будут доступны результаты статического анализа при действии заданной нагрузки и полученные критические значения в заданном диапазоне или количестве.

Настраиваем параметры расчета
После настройки NASTRAN Buckling Analysis нажимаем кнопку ОК, в окне Analysis Set Manager нажимаем кнопку Done.
Для запуска анализа можно воспользоваться иконкой
на панели инструментов или в дереве модели кликнуть правой кнопкой мыши на созданном анализе и выбрать Analyze.
Примечание:
Если в модели создано несколько различных анализов то по иконке запускается «активный».
Переключения между анализами можно производить в дереве модели двойным щелчком по тому, который должен быть «активным».
Результаты расчета
После завершения расчета на поиск собственных критических значений, результаты расчета можно посмотреть в дереве модели в ветке Results->All Result.
Переключения между результатами анализа можно производить в дереве модели двойным щелчком по тому, который должен быть «активным».
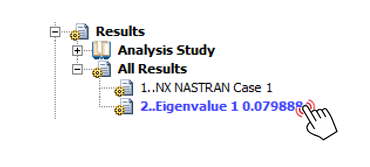
Как и говорилось ранее в ходе решения SEBUCKL 105 получены следующие результаты:
Статический анализ конструкции под нагрузкой.
Собственное критическое значение, при котором происходит потеря устойчивости.
Примечание: В соответствие с ранее выставленными настройками в NASTRAN Buckling Analysis было получено первое собственное критическое значение.
Синтаксис названия результата:
«Eigenvalue» – собственное значение;
«1» – порядковый номер;
«0.079888» – величина собственного критическое значение, коэффициент lкр.
Примечание: Величина нагрузки необходимая для достижения критического состояния конструкции определяется как произведение заданной нагрузки на полученный коэффициент lкр.
В данном примере Buckling_load FZ=10000 кН, соответственно критическая сила:
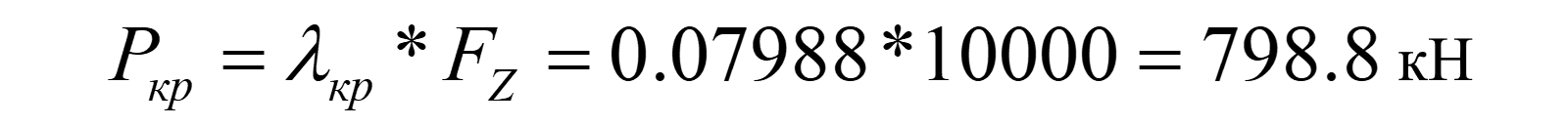
Результаты расчета
Проведем верификацию построенной модели, проверив вычисленную величину критической силы по теоретической формуле для критической силы потери устойчивости цилиндрической оболочки.
Формула имеет следующий вид:
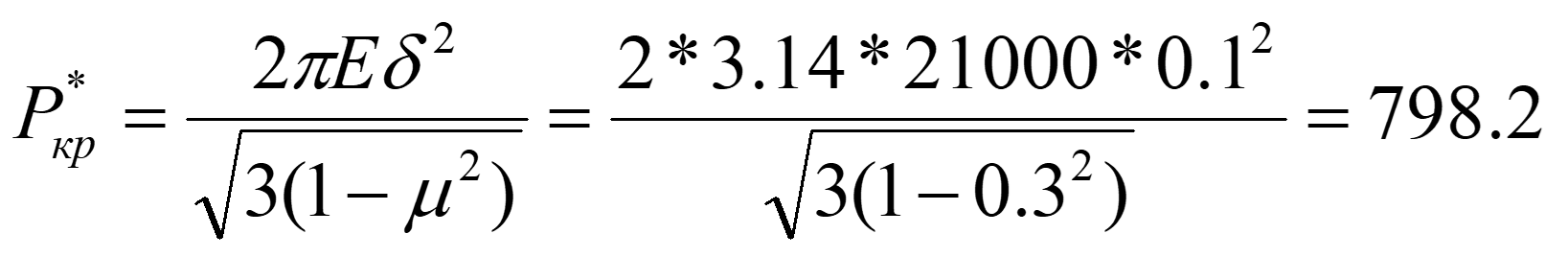
где:E- модуль упругости материала;
μ– коэффициент Пуассона;
δ–толщина стенки оболочки.

Особенности моделирования при расчетах на потерю устойчивости в линейной постановке задачи
Прежде чем приступить к проведению анализа устойчивости в линейной постановке на Вашей конечно-элементной модели убедитесь, что модель будет правильно аппроксимировать реальную конструкцию.
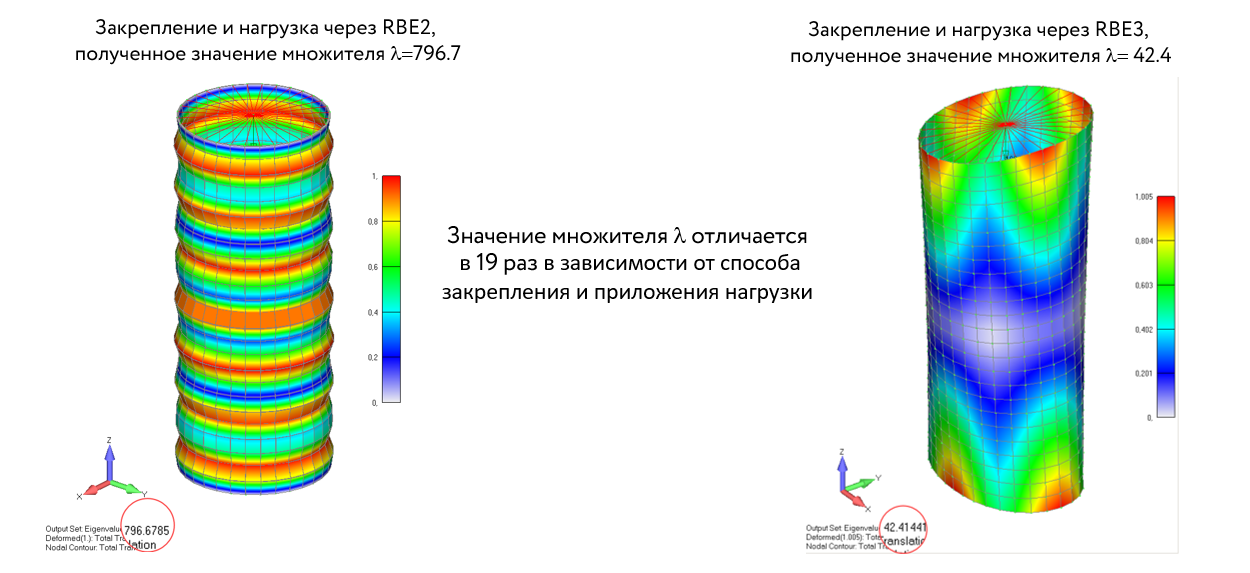
Основные факторы, которые влияют на результаты расчета:
- Качество и количество конечных элементов в модели в областях и направлениях, в которых предполагается возникновение явления потери устойчивости.
- Схема закрепления модели (фрагмента модели) и ее соответствие закреплениям реальной конструкции.
- Направление действия критической нагрузки.
Особенности моделирования

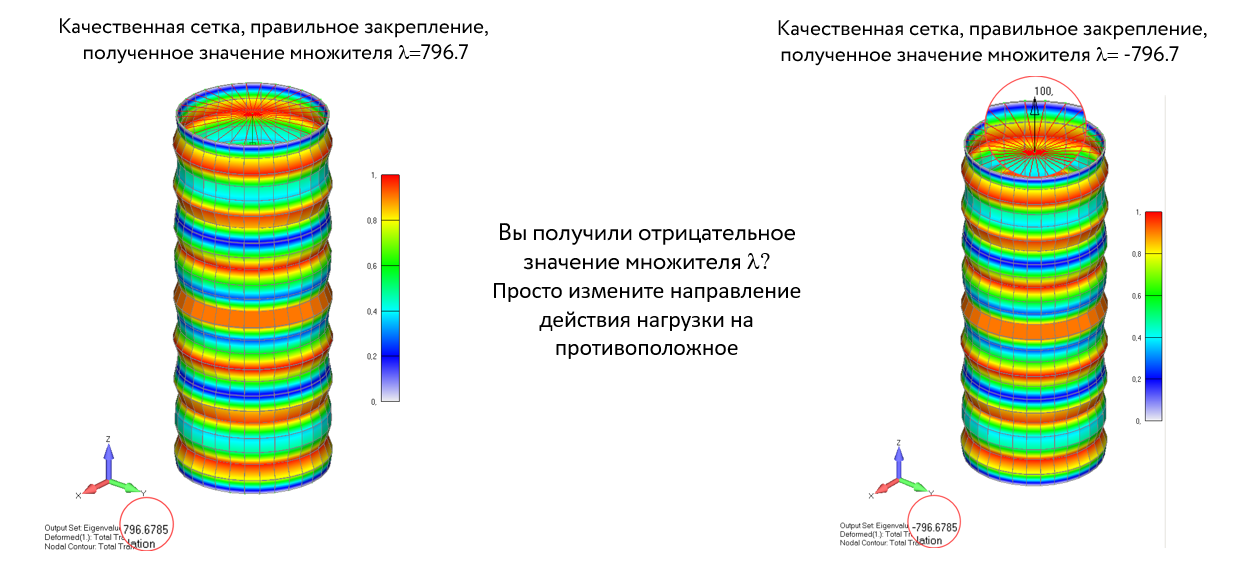
Расчет потери устойчивости цилиндрической оболочки в нелинейной постановке
В большинстве реальных конструкций отклонения от исходной конфигурации возникают с самого начала нагружения, и это не является признаком потери устойчивости. В этих условиях постановка задачи по Эйлеру дает верхнюю оценку критической нагрузки.
В отличие от метода Эйлера, которому соответствует однородное дифференциальное уравнение, здесь должно рассматриваться дифференциальное уравнение с ненулевой правой частью, то есть выполнить нелинейный деформационный анализ.
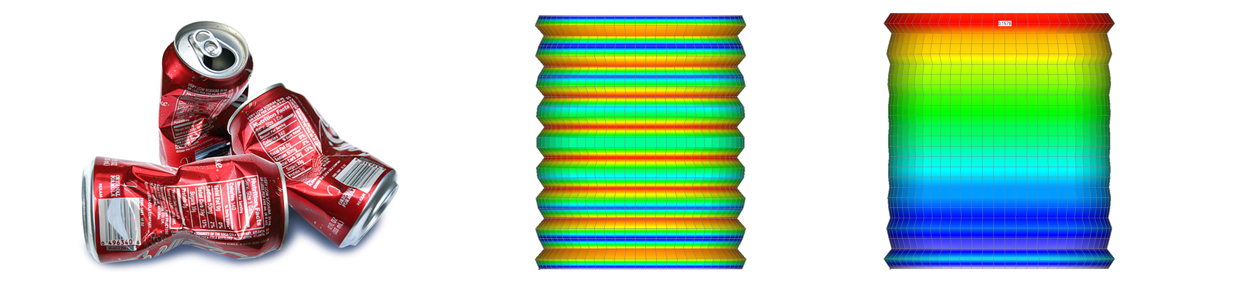
Волны формы потери устойчивости на представленном примере в линейной постановке имеют одинаковую высоту. Такой результат вызывает сомнение, поскольку не соответствует часто наблюдаемому явлению «сплющивания» цилиндрической оболочки (например тонкостенной алюминиевой банки). Исследуем потерю устойчивости этой оболочки с помощью нелинейного анализа.
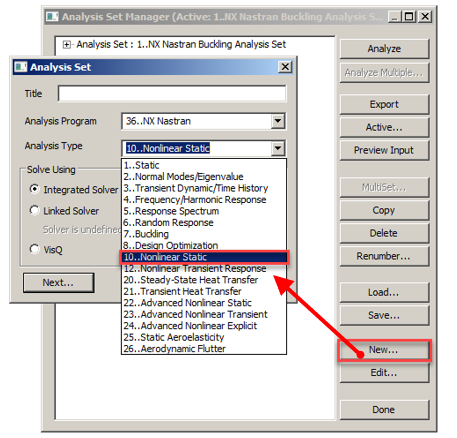
- В окне Analysis Set Manager нажимаем кнопку New;
- В окне Analysis Set выбираем тип решения (Analysis Type) –> Nonlinear Static;
- Далее кликаем кнопку Next до появления окна NASTRAN Nonlinear Static;
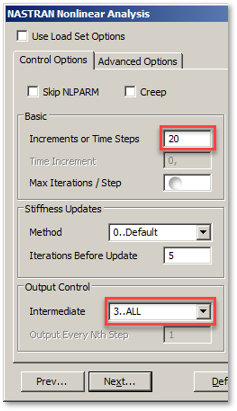
- Устанавливаем параметр Increments or Time steps в секции Basic – в Nonlinear Static отвечающий за количество шагов по приращению нагрузки/перемещения до достижения заданной величины в значение 20 шагов;
- Параметр Max Iterations/Step оставляем пустым;
- Настраиваем параметр Intermediate в секции Output Control отвечающей за запись результата на каждом шаге в значение «ALL» (то есть вывод результата для каждого шага).
- Затем кликаем кнопку Next до появления окна
- NASTRAN Output Request, устанавливаем галочку напротив Applied Load и нажимаем кнопку OK.
Настройка нелинейного расчета завершена
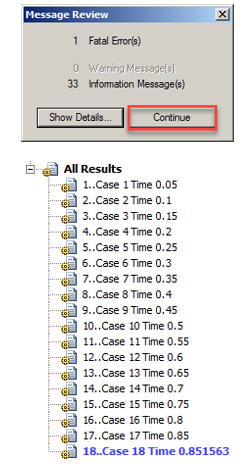
- В ходе проведения расчета получаем сообщение об ошибке и нажимаем кнопку «Continue».
- В модель загружаются результаты расчёта с 1 по 18 шаг.
- Сообщение об ошибке и получение результатов не полного решения говорит о том, что процесс нелинейного решения перестает сходиться при достижении неограниченно больших перемещений конструкции в следствие приращения на каждом шаге действующей нагрузки и, очевидно достижения ее критического значения.
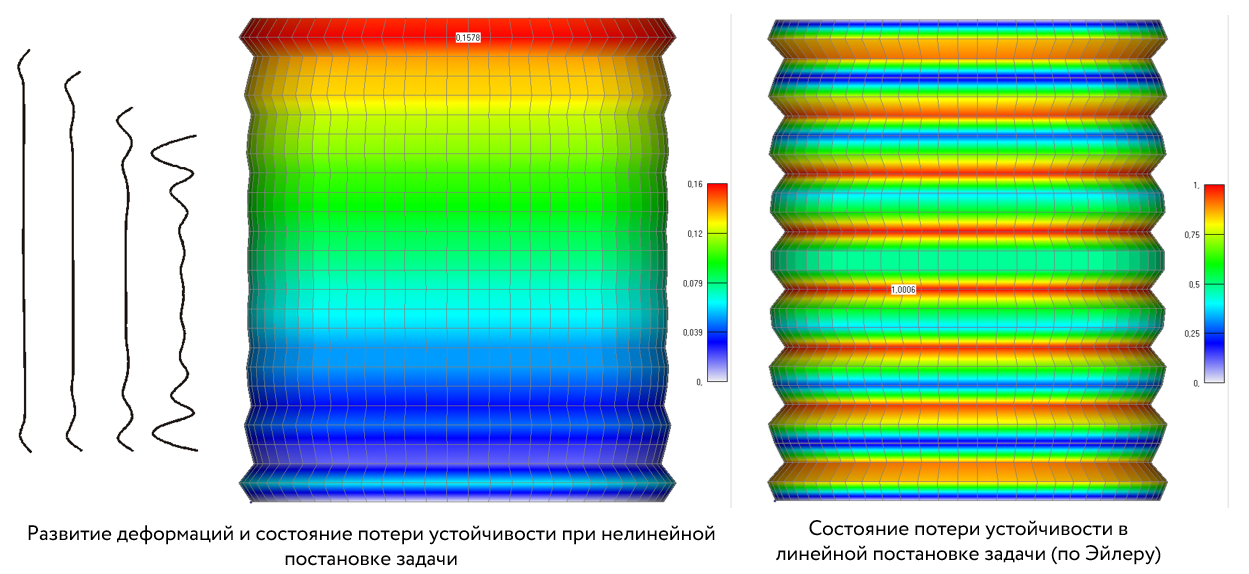
- Отобразим форму деформации при потери устойчивости в нелинейной постановке для 17 шага (для последнего шага представлен результат при котором решение уже не сошлось) в сравнении с формой деформации полученной при линейном анализе.
Для отображения используем иконки на панели инструментов:

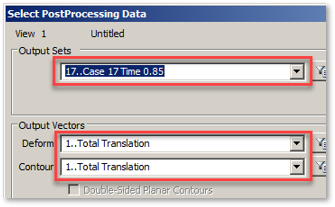
В Post Data выбираем данные о перемещениях для Case 17 Time 0.85.
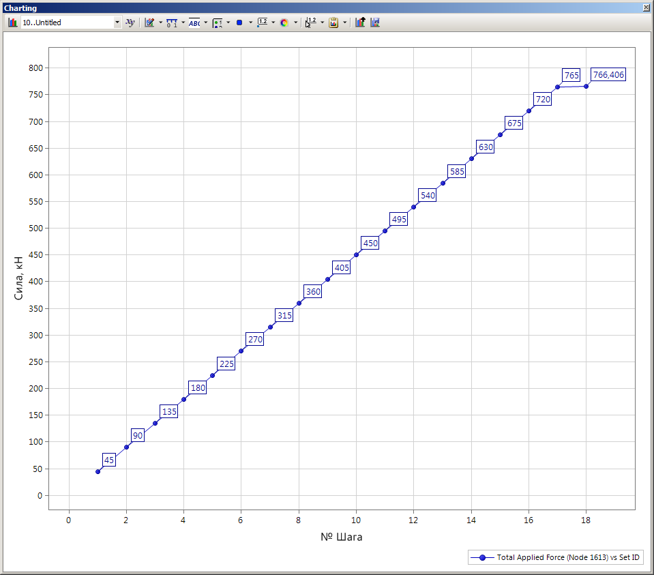
Настроим параметры отображения графика, нажав на панели инструментов на иконку Data Series Label и установив галочки напротив Display Labels и Show Y Value.
Настройки осей и самой кривой производиться с помощью интуитивно понятных инструментов, аналогичных, используемым в пакетах MS Office и требующих минимального знания английского языка.
Как видно из графика, расхождение нелинейного решения произошло при достижении на 17 шаге величины приложеннойнагрузки критического значения, равного Pкр =765 кН.
Для наглядности построим график деформаций, аналогичным способом для любого узла, где наблюдаться максимальные перемещения.
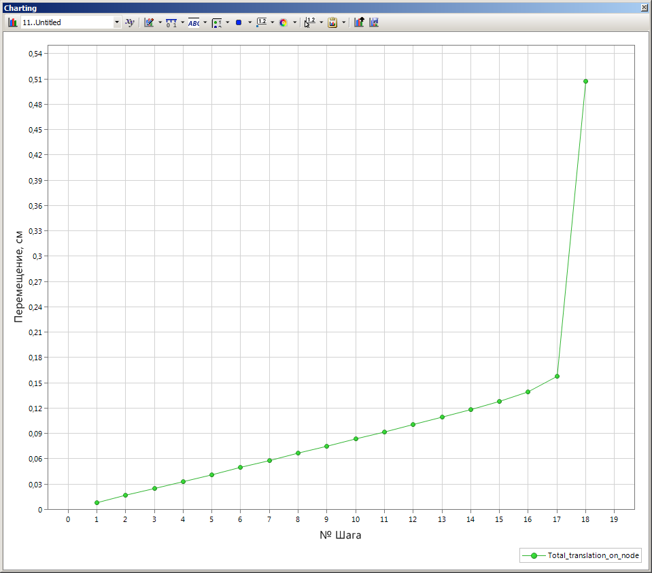
Как видно из графика, расхождение нелинейного решения происходит в следствие неконтролируемого значительного увеличения перемещений точки лежащей на вершине первой волны от торца оболочки.
Сравним полученные результаты решений в линейной и не линейной постановке:
Ркр.лн.= 798.8 кН.
Ркр.нлн.= 765.0 кН.
Разница между полученными результатами составляет 4%, при этом решение задачи по Эйлеру дает верхнюю оценку критической силы, такая разница в результатах как правило перекрывается нормативами по коэффициентам запаса устойчивости.
Выбор метода оценки устойчивости остаётся за пользователем, при этом следует также учесть что, если при моделировании используются элементы, обладающие нелинейными свойствами (Slide Line, GAP, DOF Spring), то в Buckling анализе одни из них игнорируются (Slide Line, GAP), другие линеаризуются (DOF Spring).
Расчет потери устойчивости пластины, нагруженной растягивающей силой
Решаем задачу потери устойчивости в линейной постановке. Очевидно, что в данной задаче (действует растягивающая нагрузка) минимальное собственное значение будет соответствовать сжимающей нагрузке и результатом расчета решателем при заданных граничных условиях будут являться отрицательные собственные значения.
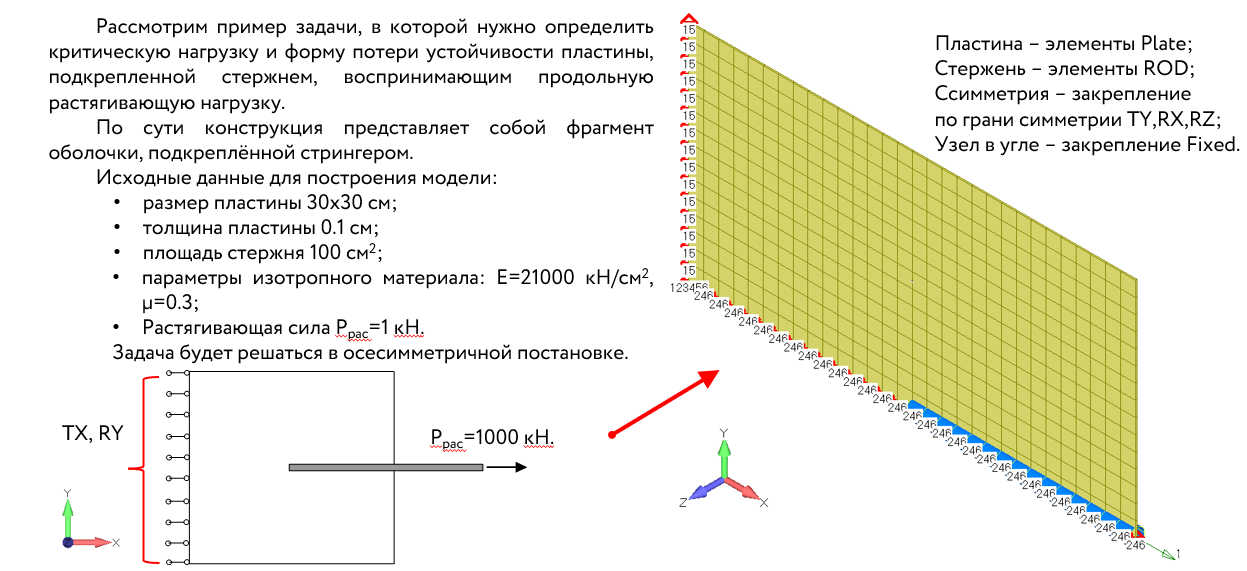
Для исключения поиска собственных значений, обусловленных сжимающей нагрузкой, необходимо настроить параметры Buckling анализа в правой части окна NASTRAN Buckling Analysis.
В области Range of Interest устанавливаем параметр From (lкр.min) равный 0.01 (ноль по умолчанию, указывает что нижняя граница поисках собственных значений не задана). Параметр To (lкр.max) оставляем по умолчанию, равным 0.
Также, в отличие от тестовой задачи с оболочкой, зададим количество вычисляемых собственных значений. Для этого в области Eigenvalues and Eigenvectors устанавливаем параметр Number Desired (a) равный 10 – количество вычисляемых корней.
При задании всех трех параметров одновременно условия для поиска собственных значений могут оказаться невыполнимыми, поэтому задать можно только одну из четырех комбинаций: a ; lкр.min + lкр.max ; lкр.min + a ; lкр.max +a.
Для заданных нами условии, первым собственным критическим значением в результатах будет либо положительное собственное значение, либо будет выдано сообщение о невозможности вычисления собственных значений.
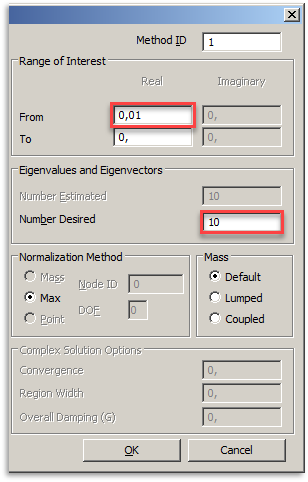
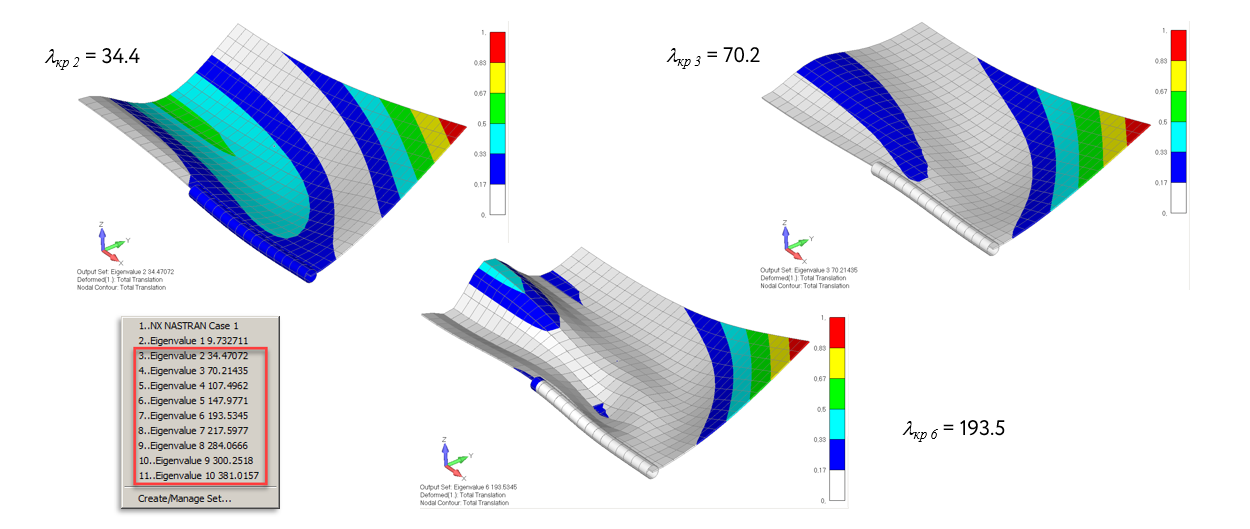
В результате решения получаем первое собственное значение lкр = 9.73 и советующую форму потери устойчивости
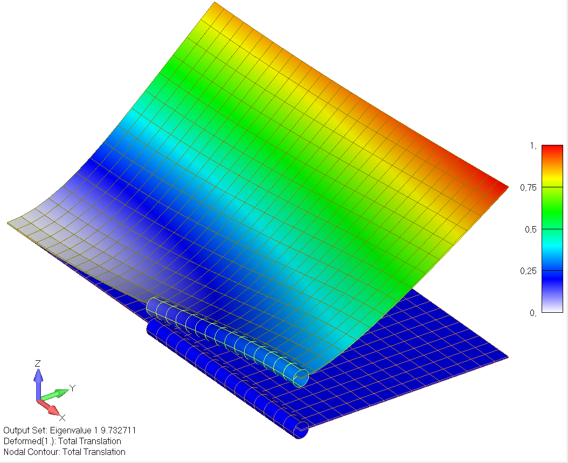
Потеря устойчивости пластины объясняется тем, что на участке пластины в центральной зоне одно из главных напряжений (MajorPrn/MinorPrn Stress) становится меньше нуля.
Поскольку в настройках решения мы задали поиск нескольких собственных значений то, можем также оценить их качественную картину.
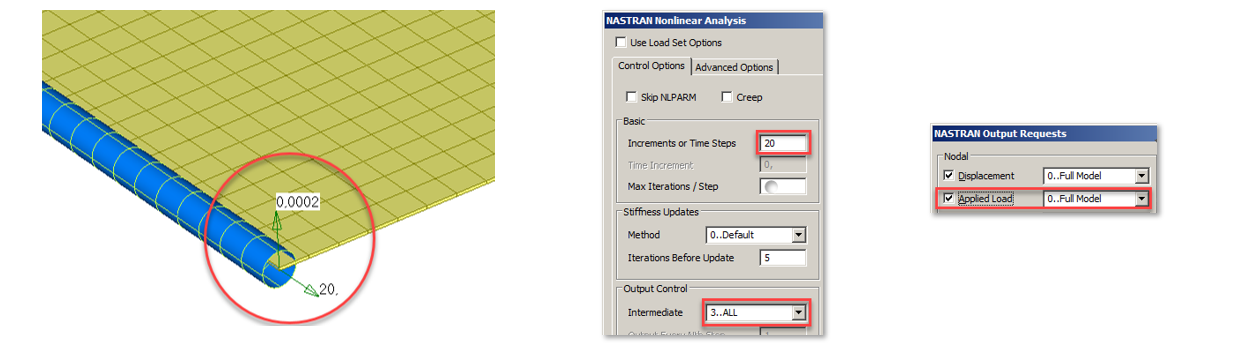
Для того, чтобы решить данную задачу в нелинейной постановке, необходимо имитировать погрешность конструкции или небольшое отклонение действующей нагрузки, в направлении «из плоскости пластины». Для этого добавляем в узел приложения нагрузки дополнительную незначительную нагрузку по оси Z. Для исключения ее существенного вклада, порядок дополнительной нагрузки должен быть 10-5…10-6 по отношению к основной действующей нагрузке.
Действующая нагрузка в нелинейной постановке, должна быть больше полученной при анализе устойчивости по Эйлеру.
Задаем: РХ = 20 кН, РZдоп. = 20 . 10-5 кН.
Настройки решателя Nonlinear Static: Increments or Time steps = 20; Intermediate=ALL; включаем Applied Load.
В результате расчета получаем все 20 результатов без ошибки, в отличие от ранее рассматриваемого случая с оболочкой. Это говорит о том, что для данной конструкции точка потери устойчивости означает лишь переход к другой равновесной форме и не приводит к потере несущей способности.
Для подтверждения построим графики перемещения точки конструкции и нагрузки и в зависимости от шага счета.
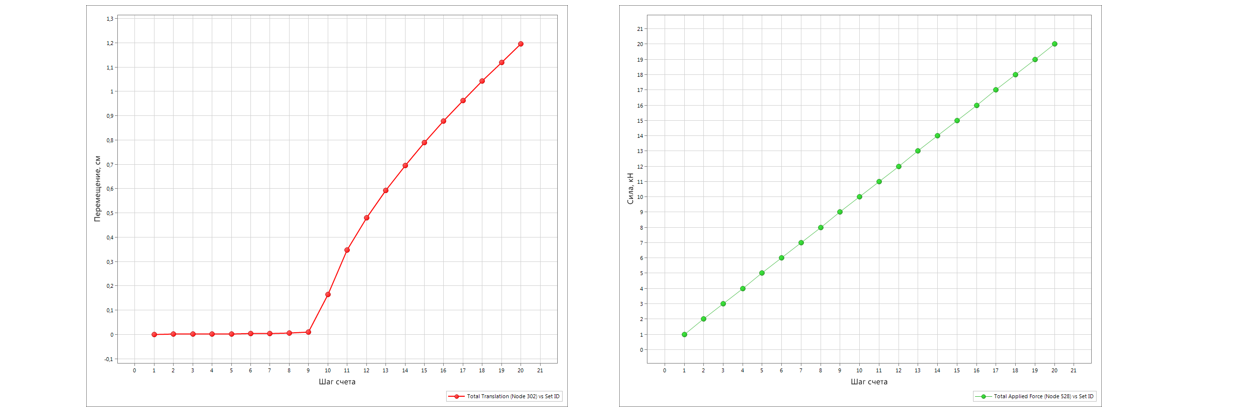
Графики стабильного роста перемещений и нагрузки подтверждают, что несущая способность конструкции сохраняется





.svg)






























.jpg)
.jpg)



