При проектировании конструкции и определении их габаритных размеров инженер-расчетчик обычно руководствуется двумя важными обстоятельствами. Первое – это несущая способность, определяемая напряжением, а вторая – статическое равновесие, степень которого зачастую контролируют с помощью расчета на потерю устойчивости. В NX Nastran есть особенности, которые как правило возникают только в случае потери устойчивости конструкций из композитов, и которые, как нам кажется, следует подробно рассмотреть. В проведенных исследованиях суть полученных результатов заключается в том, что, начиная с версии 12.2 NX Nastran (дата выпуска – сентябрь 2018 г.), лучшим способом выполнения расчета устойчивости с пластинчатыми элементами является применение элементов CQUAD4 / CTRIA3 без офсетов.
Потеря устойчивости с использованием офсетов
Первая трудность, с которой мы столкнулись, касается использования элементов с офсетами, и, хотя это обстоятельство представляет собой сложность не только для композитных материалов, оно, скорее всего, будет проблемным моментом для конструкций из композитов. При расчете деталей из композитов расчетчики часто получают CAD-геометрию для создания рабочих поверхностей, которые представляют собой OML-свойства деталей. А затем мы, как расчетчики, разумеется накладываем сетку на эти поверхности и после этого делаем офсеты элементов таким образом, чтобы нижняя часть укладки соответствовала имеющейся у нас рабочей поверхности. Применительно к элементам CQUAD4 и CQUAD8 в примечании 8 документации QRG указывается, что величина офсета (ZOFFS) не должна использоваться при вычислении дифференциальной жесткости в Solution 103, поскольку «расчет дифференциальной жесткости не учитывает направления офсетов». По правде говоря некоторые наши клиенты предпочитают использовать методику проведения анализа, где применяются элементы CQUADR, которые изначально были разработаны для того, чтобы добавить крутильную степень свободы в элемент CQUAD4.
Такая концепция заставила меня задуматься о задаче простого изгиба, которую мы разбирали в школьном курсе статической устойчивости. В задаче было показано, что приложение не осевой нагрузки к балке (как например офсет элемента) не изменяет ее собственное значение потери устойчивости в пределах линейного статического пространства. Это можно проиллюстрировать на следующем простом примере. Возьмем шарнирно опертую балку со следующими размерами:
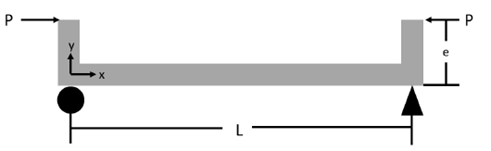
Записывая уравнение изгиба балки Эйлера-Бернулли, получаем:
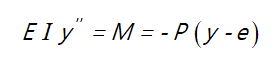
Если примем, что форма изгиба имеет вид:
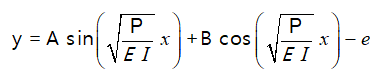
Для шарнирно опертой балки, мы знаем, что:

После определения A и B и подстановки их обратно в уравнение 2 получим:
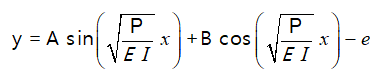
Для классической задачи потери устойчивости балки Эйлера известно, что
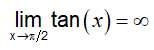
Откуда получаем:
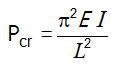
Следует отметить еще более интересный факт: эксцентриситет "e" умножается на полное решение в перемещениях уравнения 4, что означает два обстоятельства. Безусловно, мы имеем тривиальный случай, но интереснее рассмотреть концепцию о том, что независимо от значения "e" ряд перемещений будет расходиться, если будет расходиться предел тангенса. Проще говоря, параметр офсета не имеет никакого отношения к конкретному собственному значению потери устойчивости изгибающейся балки.
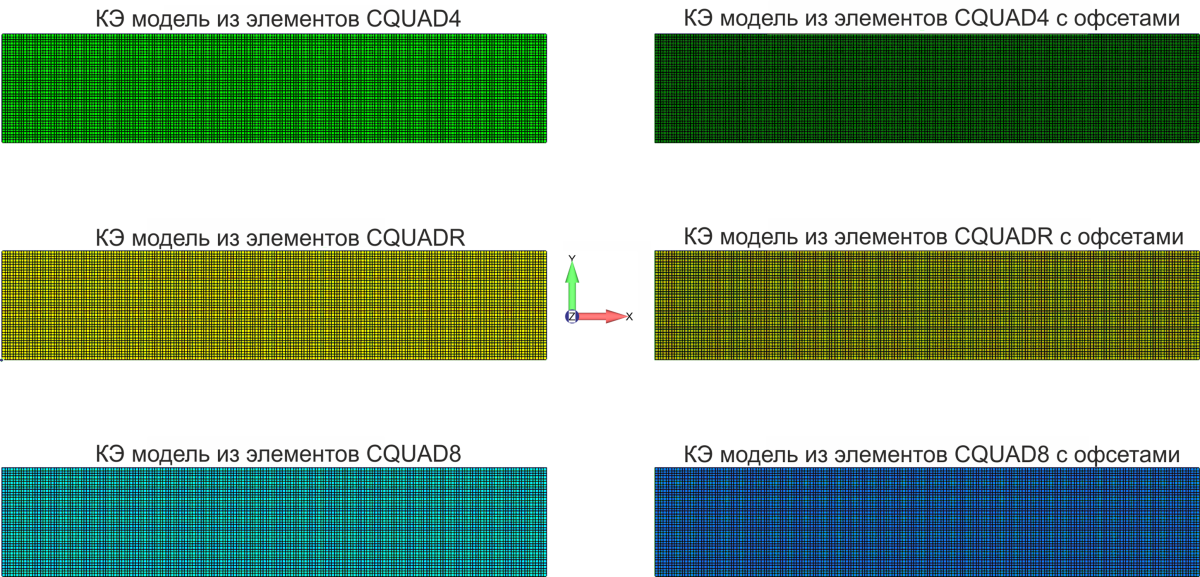
Чтобы проверить эту концепцию с помощью МКЭ, я создал шесть различных моделей прямоугольных пластин, у которые отличаются типами элементов и наличием офсетов:
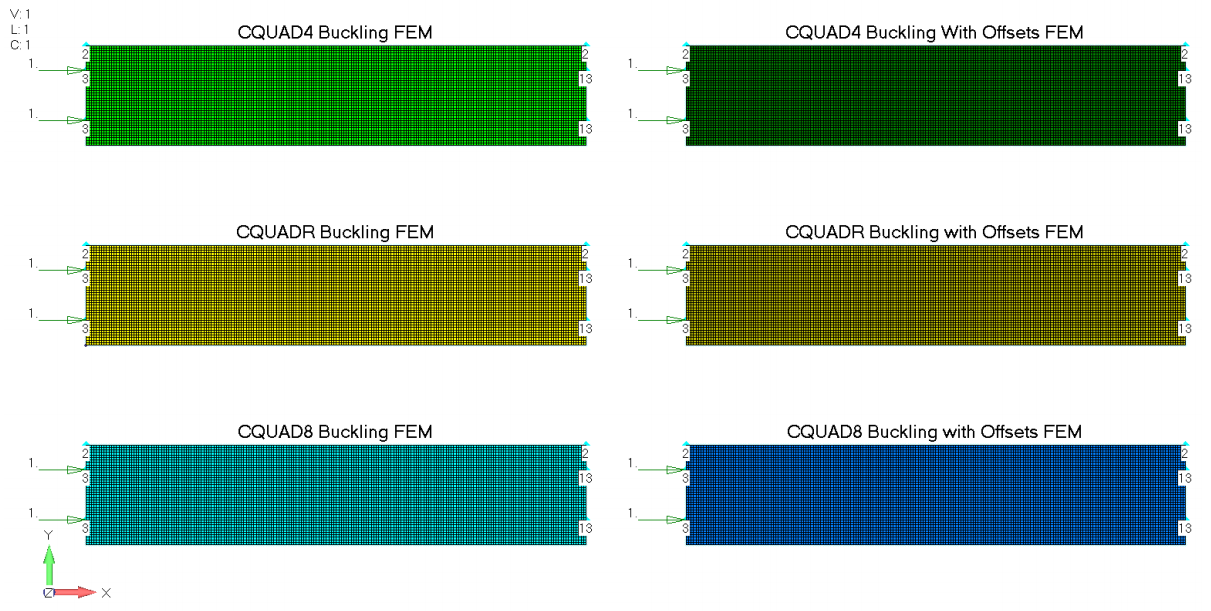
поверхностными граничными условиями для тестов на потерю устойчивости
Каждая пластина имеет размеры 1 x 5 дюйм с толщиной t = 0.05 дюйм, все пластины изготовлены из обычного алюминия с E = 10.3 ГПа.
Чтобы получить первичные данные для исследования, я сначала хотел проверить эти пластины на предмет соответствия решению задачи о потере устойчивости балки Эйлера. Для этого к пластине с одного конца прикладывалась единичная нагрузка, а каждая пластина имела шарнирное опирание. Используя уравнение 5, мы можем вычислить Pcr= 42.4 фунт:
Таблица 1: Результаты аналитического расчета балки Эйлера на потерю устойчивости
Результаты Nastran дают четкую картину и быстро выявляют причины, почему использование элементов CQUADR является более целесообразным. Все три типа элементов демонстрируют практически идентичные результаты, если к элементам модели не наложены офсеты, однако, только элементыCQUADR корректно показывают собственное значение, которое не изменяется при использовании офсетов.
Таблица2: Результаты расчета на потерю устойчивости по Эйлеру пластины с граничными условиями вертикальной балки
Для дальнейшего исследования на продольную потерю устойчивости с офсетами я хотел бы проанализировать более сложный вариант исполнения пластины, с тем допущением, что, как и в случае с вертикальной балкой, на линейные собственные значения потери устойчивости пластины не должно влиять введение офсетов. Взяв те же шесть пластин, я создал анализ на потерю устойчивости, в котором использовал граничные условия и нагружение из приведенной выше задачи об устойчивости балки Эйлера, где вычислял внутренние сжимающие нагрузки, а затем для решения задачи о собственных значениях приложил новое шарнирное закрепление, представленное ниже.
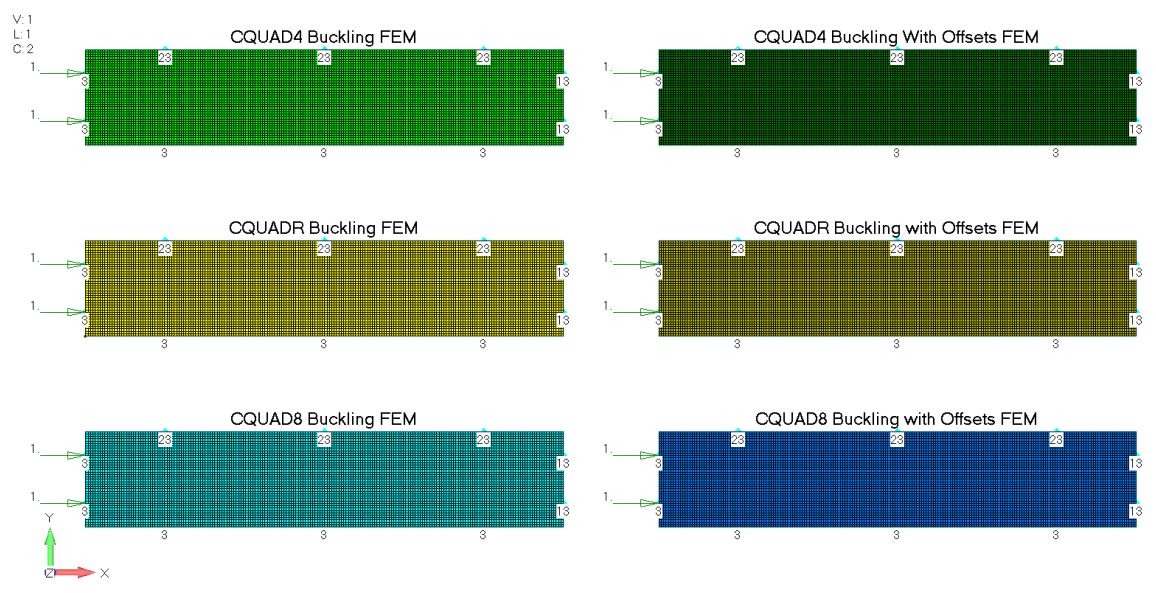
исследования на потерю устойчивости
Причина использования различных граничных условий для статической части решения и части с собственными значениями заключалась в том, что для пластин с офсетами следовало обеспечить отсутствие в местах крепления сжимающих сил в направлении оси Y. Например, когда панель имеет смещение, и прикладывается сжимающая в направлении оси X нагрузка, то из-за действия поверхностных/изгибных моментов в пластине также будет возникать существенное усилие Ny.

Для аналитического решения данной задачи я использовал уравнение C5.1, приведенное в главе C5 книги Bruhn`а:
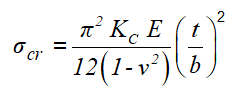
Для шарнирно опертой пластины и соотношением сторон равным 5, KC = 4. Чтобы получить критическую нагрузку, критическое напряжение может быть умножено на площадь поперечного сечения b*t, и это говорит о том, что для данной пластины критическая нагрузка потери устойчивости составляет Pcr= 4753 фунт:
Таблица 3: Результаты аналитического решения задачи о потере устойчивости пластины
И вновь элементы CQUAD4 и CQUAD8 не в состоянии продемонстрировать корректное решение задачи о потере устойчивости при использовании офсетов, а пластина из элементов CQUAD8 без офсетов даже не может выявить правильное решение. Этот результат представляет для меня сильное разочарование по двум причинам. Во-первых, я всегда был истинным сторонником использования элементов более высокого порядка, поскольку они дают более точные результаты при тех же степенях свободы, но очевидно, это не так. Во-вторых, очевидно, что-тоне то с элементом CQUAD8, вероятно, в его геометрической матрице жесткости. Пока эта ошибка не будет исправлена, я не могу рекомендовать кому-либо использовать этот элемент. Кроме этого, проведенный тест показал довольно схожие результаты с результатами расчета на потерю устойчивости вертикальной балки при использовании элементов CQUADR, продемонстрировав примерно такое же собственное значение и с офсетами, и без них, а использование элементов CQUAD4 без офсетов всего лишь дает корректное собственное значение.
Таблица 4: Результаты расчета на продольную потерю устойчивости пластины с шарнирным опиранием
В качестве еще одного пояснения для тех, кого может беспокоить погрешность ~ 4%, создаваемая элементами CQUAD4 и CQUADR без офсетов, отметим, что это вероятно потому, что в направлении y начинают оказывать влияние величина соотношения b/t = 20 и толщина пластины (проявление эффектов от сдвиговых деформаций), делая аналитическое решение Bruhn`а чрезмерно жестким, поскольку для него принимается состояние чистого изгиба.
В заключение, я хотел сравнить решения задачи о продольной потере устойчивости, которые получены на этих пластинах при действии сдвиговой нагрузки.
Аналитическое решение (уравнение C5.4) такой задачи можно также найти в книге Bruhn`а в главе C5:
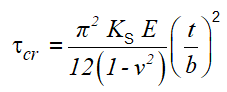
Использовав те же шесть пластин, я создал анализ на потерю устойчивости, в котором прикладывалась единичная нагрузка, линейно распределенная по периметру пластины, и предназначенная для реализации единичного усилия Nxy. Также пластины были закреплены по периметру в направлении T3 и шарнирно закреплены вдоль одной из кромок:

условиями, препятствующими сдвигу, для исследования на потерю
устойчивости
Для шарнирно опертой пластины с соотношением сторон 5, KC= 5.5. Чтобы получить фактическую критическую нагрузку, критическое напряжение может быть умножено на толщину поперечного сечения t, и это говорит о том, что для данной пластины фактическая критическая нагрузка потери устойчивости составляет Pcr= 52287 фунт/дюйм:
Таблица 5: Результаты аналитического расчета пластины на потерю устойчивости при сдвиге
Весьма примечательно, что в этом случае и элементыCQUAD4, и элементы CQUADR демонстрируют корректные собственные значения потери устойчивости как с офсетами, так и без них.
Таблица 6: Результаты расчета на потерю устойчивости пластины с
шарнирными граничными условиями при действии сдвигающей нагрузки
Однако следует отметить, что элементы CQUAD4 с офсетами дают несколько “негодных” решений. Ниже приведено сравнение формы потери устойчивости элементов CQUADR с офсетами, совместно с несколькими формами потери устойчивости элементов CQUAD4:
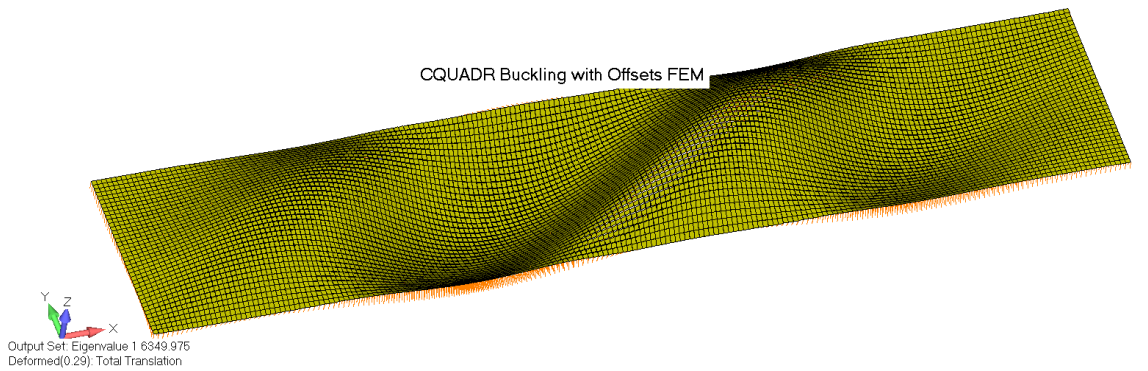

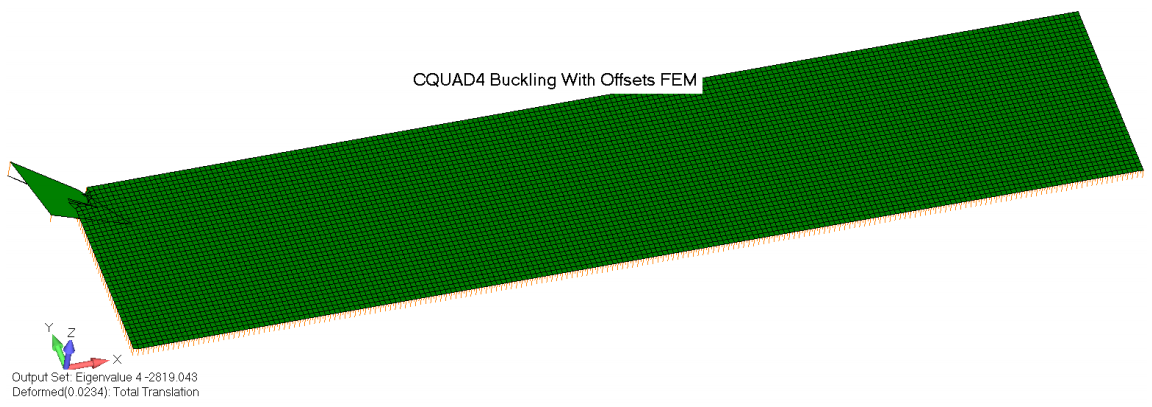

В контексте этих трех задач о потере устойчивости кажется будто единственный способ точно проанализировать устойчивость с помощью пластинчатых элементов – это смоделировать конструкцию элементами CQUAD4 по срединной плоскости или осуществлять моделирование в этих задачах элементами CQUADR.
Потеря устойчивости при наличии наполнителя
Другой распространенной особенностью композитных конструкций является внедрение в состав укладки наполнителя для увеличения жесткости на изгиб EI и для того, чтобы улучшить способность конструкции сопротивляться потере устойчивости. К сожалению, поскольку наполнитель очень податлив, это обстоятельство может привести к тому, что панель будет иметь значительно меньшую жесткость на сдвиг. В ходе нескольких уникальных проектов многие сотрудники нашей группы заметили коротковолновые изгибы на панелях с наполнителем, однако у нас не было возможности определить, возникают ли они на самом деле, и что они могут означать. Чтобы исследовать, как жесткость на поперечный сдвиг влияет на поведение конструкции при потере продольной устойчивости, я вернулся к задаче о пластине с шарнирным опиранием, при решении которой соответствующая критическая нагрузка для балки Эйлера равна 338.9 фунт. Дифференциальные уравнения, определяющие потерю устойчивости балки от сдвига, имеют вид:
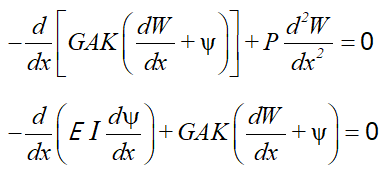
Применив эти уравнения из книги Reddy “Intro to FEA” (“Введение в МКЭ”) для балки с деформациями сдвига, мы можем получить матрицы жесткости, если используем схему с сокращенным интегрированием, чтобы справиться с завышением жесткости элементов при сдвиге:
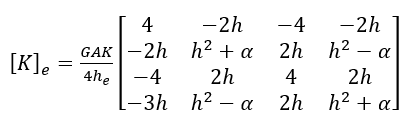
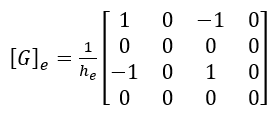
где a=EI/GAK,а h – длина элемента. Между прочим, если кто-то не знает, GAK – это сдвиговая жесткость поперечного сечения балки, и ее следует принимать во внимание только когда сдвиговой деформацией в балке нельзя пренебречь.
Полученные матрицы жесткости элементов затем могут быть скомпонованы в глобальную матрицу жесткости и использованы для вычисления критических собственных значений потери устойчивости. Для простого прямоугольного поперечного сечения коэффициент сдвига составляет 5/6, и следовательно для этого поперечного сечения мы имеем, что:
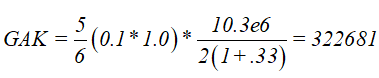
Если мы используем 20 балочных элементов, чтобы смоделировать профиль шарнирно опертой пластины, мы получим Pcr= 42.5 с представленной ниже формой потери устойчивости:
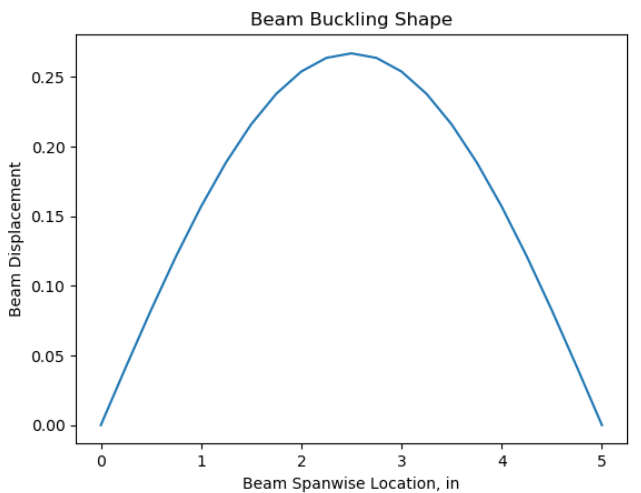
На основании этих результатов мы можем сформулировать две концепции. Во-первых, приятно видеть, что аналитическое решение задачи о потере устойчивости балки Эйлера, решение по МКЭ для пластины с элементами CQUAD и решение по МКЭ для деформируемой от сдвига балки, все они дают приблизительно одинаковые результаты. Второе и более тонкое замечание, которое мы можем сделать, заключается в том, что, как и следовало ожидать, из-за L/t > 10 мы не рассчитывали получить существенных проявлений деформации сдвига.
Напрашивается вопрос: что произойдет с собственным значением потери устойчивости, если мы принудительно уменьшим жесткость на поперечный сдвиг? Ниже представлен график зависимости критического собственного значения от жесткости балки на поперечный сдвиг:
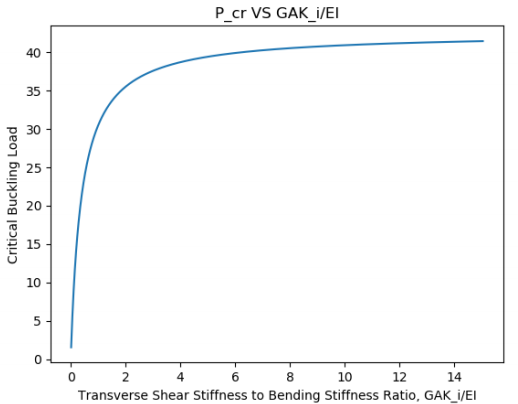
устойчивости балки Тимошенко от отношения жесткости на поперечный сдвиг к жесткости на изгиб
На основании этого графика можно сказать, что изменение только величиныGAK незначительно влияет на критическую нагрузку потери устойчивости до значения GAC=8EI, после чего критическое собственное значение резко убывает. Что еще более интересно, если мы построим график критической нагрузки потери устойчивости, приведенной к жесткости на поперечный сдвиг, мы увидим, что:
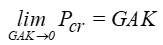
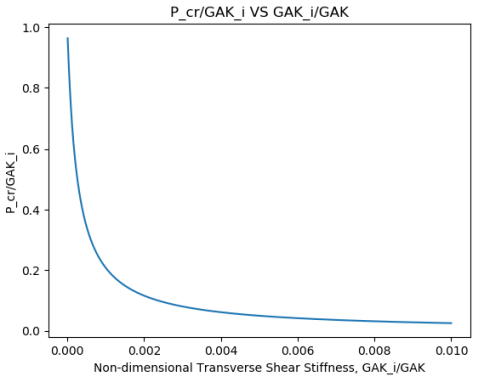
Таким образом, становится очевидно, что независимо от того, насколько гибкой является балка, если жесткость на поперечный сдвиг близка по величине к жесткости на изгиб, то на собственное значение потери устойчивости будут оказывать существенное влияние оба эти компонента. Кроме того, при GAK << EI, мы получаем два интересных результата. Во-первых, мы установили, что
Pcr= GAK. Во-вторых, мы обнаружили, что все собственные значения примерно равны жесткости на поперечный сдвиг, как это показано на рисунке ниже:
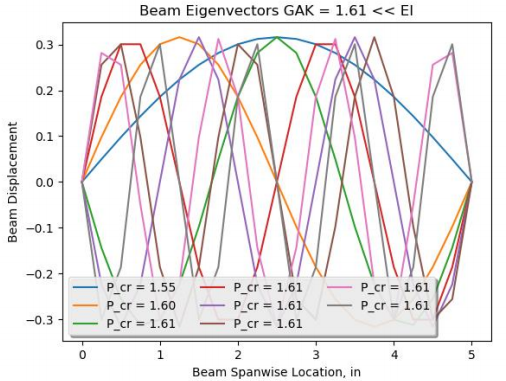
Здесь смысл заключается в том, что если для части конструкции значение GAK очень мало, то анализ потери устойчивости даст пары величин собственное значение / собственный вектор для всех степеней свободы податливой конструкции, причем все эти степени свободы будут иметь примерно одно и то же собственное значение. Вот, скорее всего, почему у панелей с наполнителем образуется так много коротковолновых изгибов, и все с примерно одинаковыми собственными значениями.
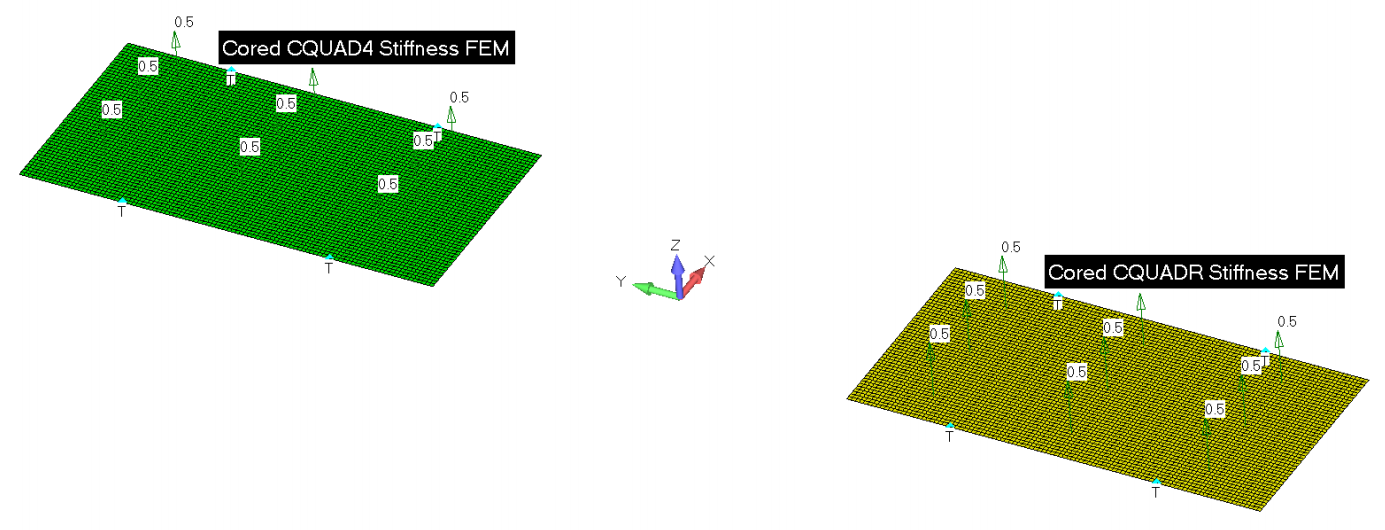
Случайно, я заметил, что даже когда на элементы не наложены офсеты, при моделировании панелей с наполнителем элементы CQUAD4 и CQUADR демонстрируют существенно отличающиеся собственные значения. Чтобы выяснить, почему такое возможно для панелей с наполнителем, рассмотрим 4 толстых пластины, с габаритными размерами 1.0x0.5 дюйм. Пластины предназначены для того, чтобы отобразить результаты действия поперечного сдвига:
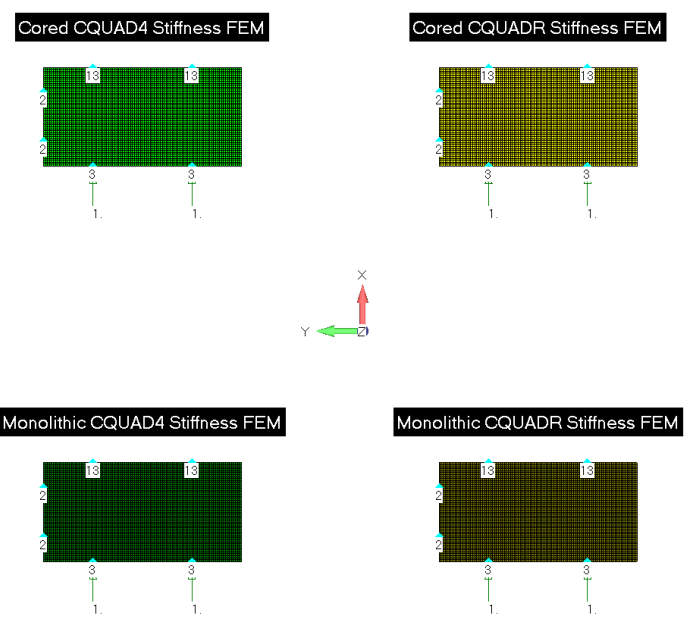
Укладка для двух нижних пластин имеет вид [0 / 45_2 / 0_2 / 45_2 / 0_2 / 45_2 / 0] _s, где все слои представляют собой типичную графитовую ткань с толщиной слоя 0.008 дюйм и следующими характеристиками материала:
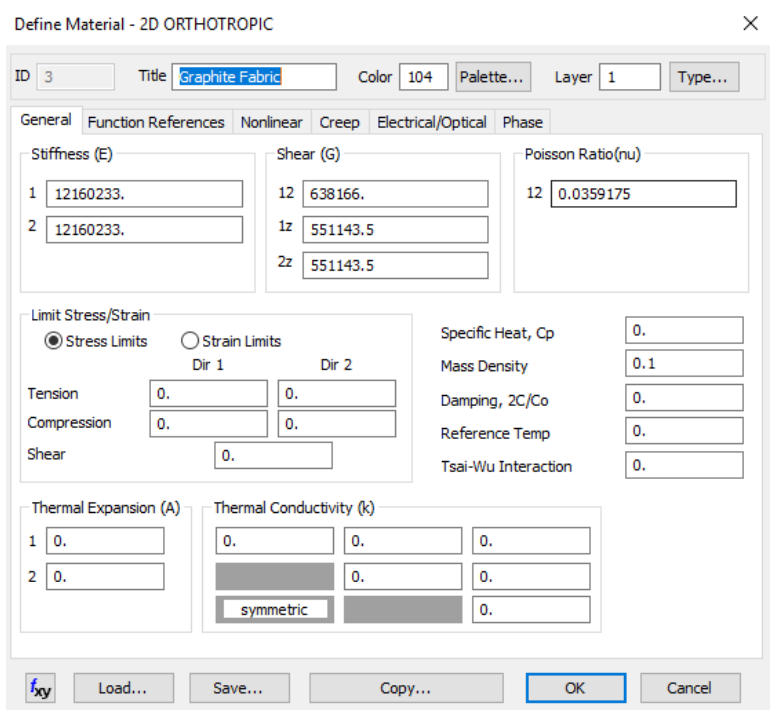
Укладка верхнего ряда для панелей с наполнителем имеет вид [0 / 45_2 / 0 / сердечник /0 / 45_2 / 0], где наполнитель представляет собой сотовые ячейки Hexcel 1/8 с плотностью 3 фунт/фут3 и толщиной 1/8 дюйм. Для других слоев в укладке с наполнителем используется графитовая ткань, характеристики которой представлены выше.
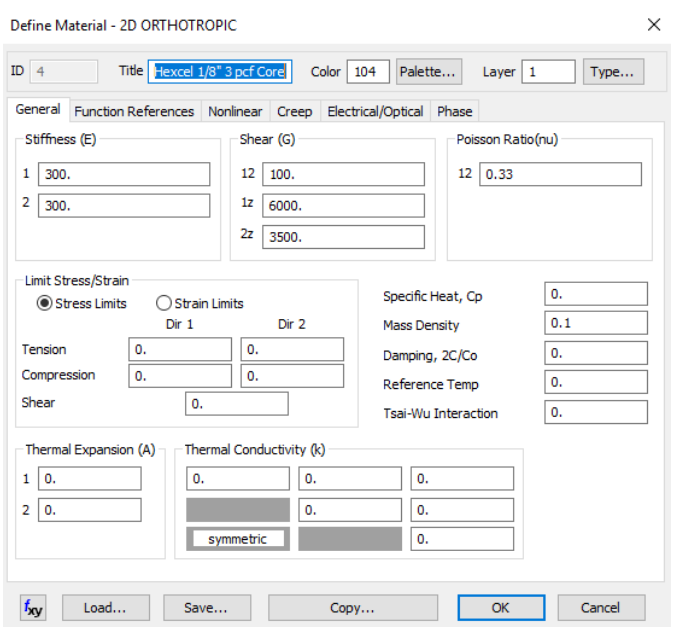
Последнее, что следует отметить: к каждой пластине прикладывается единичная сжимающая нагрузка, и на них наложены те же шарнирные закрепления, которые ранее использовались для металлических пластин. С учетом предыдущего анализа не стоит удивляться тому, что без офсетов сплошные панели из элементов CQUAD4 и CQUADR демонстрируют примерно одинаковые собственные значения и профиль формы потери устойчивости. Хотя еще более интересно, что панели из CQUAD4 и CQUADR с наполнителем имеют совершенно разные собственные значения:
Таблица 7: Критические собственные значения потери устойчивости для пластины с граничными условиями балки Эйлера
На основании этого обстоятельства мы можем определенно сказать, что-то не так с результатами у панели с наполнителем, сделанной и из CQUAD4,и из CQUADR, хотя неясно, какой из этих результатов правильный. На примере с деформируемой от сдвига балкой мы установили, что наличие достоверных характеристик жесткости на изгиб и поперечный сдвиг может быть важным при решении конкретных задач потери устойчивости. В связи с этим, в качестве первого шага логично будет удостовериться в корректности значений жесткости на изгиб и поперечный сдвиг панелей с наполнителем. Для этого были применены два подхода. В первом подходе панели с наполнителем были нагружены равномерно распределенной единичной нагрузкой 0.5 фунт/дюйм2, и к ним наложены граничные условия свободного опирания.
С помощью аналитического решения из книги Reddy's “Intro to FEA” (“Введение в МКЭ”), прогиб и угол поворота для деформируемой от сдвига балки можно выразить следующим образом:
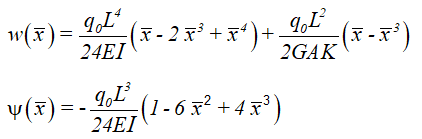
Получены следующие значения жесткостей:
Таблица 8: Значения жесткости поперечного сечения, полученные с помощью AeroComBAT
Определив прогибы и угловые смещения из КЭ модели, получаем следующие жесткости:
Таблица 9: Значения жесткостей поперечного сечения, полученные в результате расчета на КЭ модели
Посредством сравнения результатов, полученных из расчетов на AeroComBAT, с результатами NASTRAN,становится ясно, что в случае, если наполнитель (или материал со сравнительно малой жесткостью на поперечный сдвиг) входит в состав укладки, поперечная жесткость на сдвиг всего пакета некорректно определяется элементами CQUADR. Скорее всего, это обстоятельство не означает, что с наполнителем происходит что-нибудь особенное, хотя даже при чередовании материалов в пакете слоев поперечная жесткость на сдвиг неправильно вычисляется элементами CQUADR. Этой неточностью можно пренебречь, если все материалы в укладке будут иметь одинаковую или примерно одинаковую жесткость на поперечный сдвиг. Мне кажется, что жесткость на поперечный сдвиг наружных листов также неверна, если листы моделируются элементами CQUADR, поскольку они, вероятно, будут смещать значение поперечной жесткости на сдвиг ближе к наиболее податливым слоям в пакете.
Один из более важных выводов из приведенного выше примера с деформируемой от сдвига балкой заключается в том, что, когда значение GAK очень мало по сравнению с EI,то величина критической силы Pcr= GAK, которую мы как раз и находим в этой задаче. Собственные значения потери устойчивости для каждой пластины с наполнителем практически полностью совпадают с величинами жесткости на поперечный сдвиг, вычисленными для каждой панели по отдельности. Это также приводит к распространенному заблуждению о том, что образование изгибов (и, в особенности, коротковолновых изгибов) на панелях с наполнителем, является результатом поперечного обжатия, которое представляет собой коротковолновую подвижность наполнителя, с фактической критической нагрузкой, рассчитываемой по выражению:
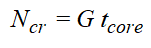
где G – модуль поперечного сдвига наполнителя, а tcore– толщина наполнителя. Для представленных выше пластин критическая сила поперечного обжатия
Ncr= 6000 (0.125) = 750 фунтов/дюйм, которая в данном случае близка к собственному значению, определённому с помощью элементов CQUADR. Может быть, это просто совпадение, поскольку жесткость на поперечный сдвиг элементов CQUADR значительно ближе по величине смещена к показателям самого податливого материала в пакете, что некорректно. Иными словами, невозможно достоверно установить связь между коротковолновыми изгибами, которые возникают при обжатии наполнителя, и которые наблюдаются в результатах анализа с NX Nastran.
Резюме
Полученные в данной статье результаты способны немного обескуражить любого инженера-прочниста, который рассчитывает композитные конструкции в NX Nastran. Из первого раздела ясно, что только элементы CQUADR правильно работают с офсетами. Однако во втором разделе обнаружено, что элементы CQUADR имеют некорректную жесткость на поперечный сдвиг, поэтому единственно верный способ произвести анализ устойчивости композитных конструкций – это выполнить его с использованием элементов CQUAD4 без офсетов. Хотя получаемые результаты и вносят ясность в некоторые тонкости процесса потери устойчивости, они не дают ответа на вопрос, являются ли реальными коротковолновые изгибы, которые обнаруживаются на панелях с наполнителем при расчете в NXNastran, и, если это так, в чем заключается их физический смысл. Зачастую, возникновение этих коротковолновых изгибов сильно зависит от качества сетки. Например, если при обнаружении этих коротковолновых изгибов на панели откорректировать сетку, удвоив количество узлов, то собственная форма будет иметь аналогичный профиль с удвоенным количеством точек перегиба при почти таком же собственном значении. Такое непостоянное решение, которое зависит от сетки, является весьма характерным признаком проблемы сходимости численных методов. Я бы рекомендовал не учитывать эти собственные значения, хотя было бы лучше исключить их рассмотрения на основании изучения вопроса о достоверности по результатам нелинейного анализа.





.svg)




























.jpg)
.jpg)



