Femap. Частотный анализ отклика

Общие сведения

Частотный анализ (4..Frequency/Harmonic Response) – нахождение установившейся реакции конструкции на гармоническое возбуждение. В случае гармонического возбуждения все внешние силы должны быть явно определены для всех частот возбуждения.

Для установившегося колебательного процесса характерно, что все степени свободы системы движутся с одинаковой частотой. Отклик системы может не совпадать по фазе с внешним воздействием. Причиной возникновения сдвига по фазе является наличие демпфирования.

Результаты частотного анализа находятся в комплексных числах. Существует возможность вывода как амплитуды и фазы, так и действительной и мнимой частей. Комплексные перемещения имеют вид:

где U0 – амплитуда перемещений;

U0cos – действительная часть вектора перемещений;

U0sin – мнимая часть вектора перемещений.

Для решения частотного анализа в решателе NX Nastran реализованы два метода:

• Прямой метод–решение SEDFREQ 108 (Direct Frequency Response анализ)
• Модальный метод– решениеSEMFREQ111 (Modal Frequency Response анализ).

Выбор метода зависит от размерности исследуемой системы, необходимой точности результатов, количества частот возбуждения, необходимости проведения анализа в высокочастотной области и прочего.

Прямой метод

При использовании метода прямого интегрирования отклик системы определяется на каждой отдельной частоте возбуждения посредством решения уравнений движения с помощью комплексной алгебры.

Уравнение движения установившихся вынужденных колебаний системы с учетом ее диссипативных свойств имеет вид:

Вектор внешних нагрузок, представленный в правой части уравнения, так же как и вектор реакции системы, имеет комплексную форму. Решением уравнения является:

Взяв первую и вторую производные от перемещения по времени, подставив в уравнение и сократив на e^iwt, получим выражение:

Выбор частот

Для нахождения отклика конструкции уравнение движения решается для каждой отдельной частоты возбуждения (то есть набор уравнений с разными частотами возбуждения) аналогично решению уравнений статического равновесия с использованием комплексной алгебры.

В решателе NX Nastran существуют шесть параметров выбора частот, для которых ищется решение:

• FREQ
• FREQ1
• FREQ2
• FREQ3
• FREQ4
• FREQ5

• FREQ – задание дискретных частот возбуждения;
• FREQ1 – определение набора частот возбуждения посредством задания начальной частоты, частотного приращения и количества частотных приращений;
• FREQ2 – определение набора частот возбуждения посредством задания начальной, конечной частот и количества логарифмических приращений;
• FREQ3 – задание количества частот возбуждения между двумя собственными частотами в диапазоне между начальной и конечной частотами;
• FREQ4 – определение набора частот возбуждения посредством задания начальной, конечной частот, диапазона в окрестности каждой собственной частоты и числа равномерно распределенных частот в этом диапазоне;
• FREQ5 – определение набора частот возбуждения посредством задания начальной и конечной частот и набора долей от собственных частот системы.

Демпфирование

Демпфирование системы для прямого метода частотного анализа представлено матрицей [B], характеризующей вязкое демпфирование отдельных типов конечных элементов CVISC, CDAMPi, CBUSH, CELASi, и комплексной матрицей жесткости [K], включающей как жесткость системы, так и структурное демпфирование.

При этом для частотного анализа структурное демпфирование, задаваемое через параметр PARAM,G и коэффициент конструкционного демпфирования свойств материала GE, не определяет непосредственно саму матрицу демпфирования, а формирует глобальную комплексную матрицу жесткости:

где [K] – глобальная комплексная матрица жесткости;

G – общий коэффициент структурного демпфирования (PARAM,G);

[KE] – матрица жесткости элементов;

GE – коэффициент конструкционного демпфирования элементов (GE).

Коэффициенты структурного демпфирования автоматически добавляются в матрицу жесткости и, соответственно, учитываются при решении уравнений движения.

Следует отметить, что в одном решении могут быть использованы все типы демпфирования.

В отличие от переходного анализа, существует возможность использовать комплексную матрицу жесткости, поэтому не требуется преобразования структурного демпфирования в эквивалентное вязкое.

Коэффициент конструкционного демпфирования (Structural Damping Coefficient) G является безразмерной величиной и характеризует работу всех диссипативных сил, рассеиваемую за один цикл колебаний. Эквивалентный коэффициент вязкого демпфирования (Viscous Damping Coefficient) C характеризует работу, совершаемую силами вязкого демпфирования и рассеиваемую за один цикл колебаний.

Считая эти потери эквивалентными, можно выразить коэффициент C через коэффициент G. Для системы с одной степенью свободы это выражение имеет вид:

где k – жесткость системы, ω – собственная круговая частота колебаний системы с демпфированием. Для систем с малым демпфированием ω ≈ ωn, где ωn – собственная круговая частота колебаний без демпфирования.

Критический коэффициент вязкого демпфирования (Cкр) характеризует степень вязкого демпфирования, при котором движение системы впервые начинает терять свой колебательный характер. Для системы с одной степенью свободы, массой m и жесткостью k этот коэффициент определяется как:

Эквивалентное значение коэффициента вязкого демпфирования (ζ) определяется как:

Для системы с одной степенью свободы справедливо соотношение:

Добротность колебательной системы (Q factor, или Amplification) – безразмерная величина, характеризующая резонансные свойства системы. Она равна отношению резонансной круговой частоты ω к ширине резонансной кривой Δω на уровне убывания амплитуды корень из двух раз: Q = ω/Δω. При действии периодической возбуждающей силы F0sinωt на механическую систему с одной степенью свободы добротность может быть определена как отношение максимальной амплитуды колебаний, когда ω ≈ ωn, к статическому смещению под действием постоянной силы F0. Это отношение приблизительно равно:

При задании исходных данных параметры демпфирования (G, ζ и Q) задаются в частотной области, то есть в зависимости от частоты. С помощью частоты приведения они преобразуются к эквивалентному вязкому демпфированию в форме матрицы демпфирования конструкции.

Модальный метод

Альтернативным методом нахождения отклика конструкции на динамическое воздействие является модальный метод (метод суперпозиции форм колебаний), использующий найденные собственные частоты и формы свободных колебаний.

В основе данного метода лежит возможность представления деформированной формы линейно-упругой системы набором ее собственных форм колебаний, то есть переход от физических координат к модальным (обобщенным) координатам.

Если демпфированием пренебречь, то в терминах обобщенных координат и учитывая свойство ортогональности собственных форм колебаний, уравнение движения примет вид:

mi – i-aя модальная обобщенная масса;

ki – i-aя модальная обобщенная жесткость;

pi – i-aя модальная обобщенная сила.

Таким образом, уравнение движения заменяется на множество несвязанных уравнений, каждое из которых является уравнением движения системы с одной степенью свободы.

Результатом решения системы уравнений является обобщенная реакция для каждой формы колебаний.

Соответственно, после нахождения всех обобщенных координат по всем учитываемым формам определяется физический вектор перемещений путем суммирования всех реакций системы по всем модальным откликам:

При частотном анализе модальным методом как матрица демпфирования [B], так и глобальная комплексная матрица жесткости не являются диагональными, следовательно, нарушается условие независимости модальных уравнений движения. В этом случае решается система связанных уравнений методом прямого численного интегрирования аналогично частотному анализу прямым методом, но только в терминах обобщенных координат. Обычно количество обобщенных координат, используемых в модальном методе решения, значительно меньше физических, и прямое интегрирование уравнений движения не требует значительных вычислительных затрат, как в случае частотного анализа прямым методом. Однако если задать демпфирование для каждой собственной формы, то может быть использован метод разделения по формам, так как в этом случае сохраняется условие независимости собственных форм колебаний, а следовательно, условия несвязности уравнений.

Данный подход при учете демпфирования называется заданием модального демпфирования, когда каждой i-й собственной форме соответствует свое демпфирование bi. И уравнение движения для i-й собственной формы имеет вид:

Метод прямого интегрирования дает точный результат, но при увеличении размерности задачи вычислительная эффективность данного метода значительно падает. Модальный метод дает приближенное решение динамического анализа. В случае учета всех собственных

векторов системы решение получается точным, равным результату метода прямого интегрирования.

Однако, исходя из практического опыта применения модального метода, известно, что для получения корректной аппроксимации отклика системы достаточно учитывать небольшое количество ее первых собственных форм колебаний.

Рекомендуется учитывать все собственные формы системы в диапазоне, перекрывающем диапазон частот возбуждения в два и более раз.

В таблице представлены общие рекомендации при выборе метода частотного анализа.

Пример

Анализ 4..Frequency/Harmonic Response используется для определения реакции структуры на гармоническое (колебательное) возбуждение, где все силы на каждой частоте воздействия известны и определены в частотной области.

Ответы состоит из комплексных чисел, определяемых как величина и фаза или как реальные и мнимые компоненты.

• Сначала будет проведен модальный анализ модели для определения собственных форм и частот.
• Используя рестарт, который позволяет перезапускать анализ, будет выполнен гармонический анализ без повторного извлечения собственных форм и частот.

Целью данного примера является определение отклика конструкции на синусоидальную нагрузку единичной амплитуды в диапазоне частот до 600 Гц.

Этот диапазон частот выбран на основе предварительного анализа собственных форм и частот и содержит первые три частоты конструкции. Критическое демпфирование системы принято 10%.

Анализ собственных форм и частот

Анализ собственных форм и частот (2..Normal Modes/Eigenvalue) с включенной опцией «Save Databases for Restart» в разделе Restart Control в настройках анализа NASTRAN Executive and Solution Options для использования полученных результатов в последующем анализе отклика на синусоидальное воздействие.

Остальные настройки остаются по умолчанию

Number Desired=10 – в результате расчета будет вычислено первые десять собственных форм и частот. Для данной модели этот диапазон охватит больше 80% суммарной эффективной массы по всем трем направлениям X, Y и Z.

Результаты расчета собственных форм и частот

Создание функций нагрузки и демпфирования

Анализ отклика модели на синусоидальное возбуждение.

• Создание нагрузки как функции в зависимости от частоты.
• Примем единичную нагрузку постоянной величины на всем диапазоне частот от 0 до 3000 Герц.
• Создание функции демпфирования в зависимости от частоты.
• Примем критическое демпфирование 10% постоянным на всем диапазоне частот от 0 до 3000 Герц.

Приложение нагрузки

В диалоговом окне Editing Load Definition в разделе Load необходимо задать нагрузку как функцию от частоты

Настройки анализа

В диалоговом окне Analysis Set в поле типа анализа выберите анализ отклика на синусоидальное воздействие 4..Frequency/Harmonic Response

В диалоговом окне NASTRAN Executive and Solution Options в разделе Restart Control активируйте опцию рестарта с предыдущего анализа Restart Previous Analysis и в поле From укажите путь к файлу рестарта .MASTER

В диалоговом окне NASTRAN Modal Analysis в разделе Solution Type выберите модальный способ решения Modal.

В диалоговом окне NASTRAN Dynamic Analysis в поле Modal Damping задайте график демпфирования.

В разделе Frequency Response нажмите кнопку Modal Freq, чтобы создать список частот для анализа.

Этот график показывает три пика, один пик для каждого из первых трех мод собственных колебаний. Значение Y произвольно на этой диаграмме, но Х-значения являются отличным способом визуализировать, где происходят возбуждения по отношению к частотному диапазону. Кроме того, ширина основания каждого пика представляет собой полосу частот, используемую в решении гармонического анализа.

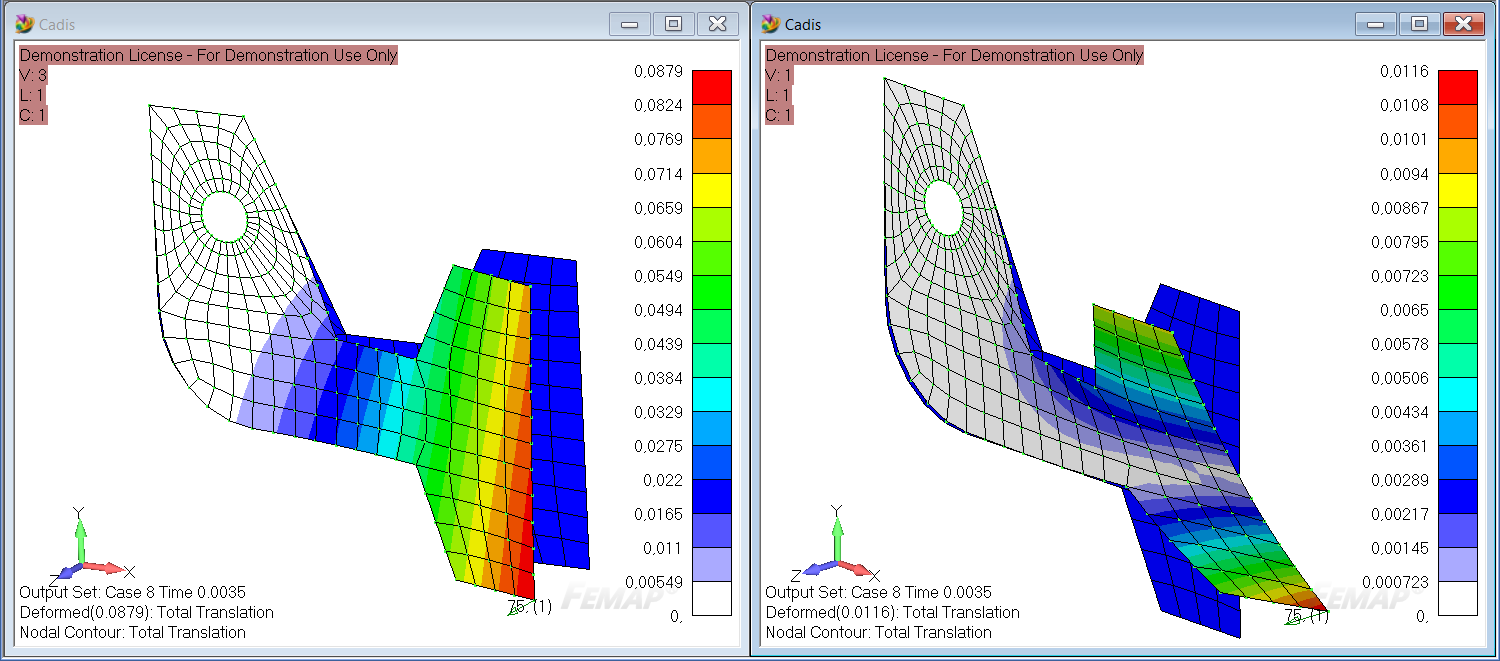
Анализ результатов

На рисунке изображен график зависимости перемещений узла 44 от частоты и график с выбранными частотами, показанный на предыдущем слайде (в масштабе 1/1000).

Таким образом по диаграмме можно оценить преимущества модального метода – на каждом резонансном пике с шириной 10% (Frequency Band Spread) был посчитан отклик конструкции по 5 точкам (Number of Points per Existing Mode).

При увеличении ширины Frequency Band Spread и количества расчетных точек Number of Points per Existing Mode  можно расширить диапазон точного решения.

Обратите внимание, что точность максимального отклика на резонансных частотах не зависит от этих параметров.