Общее описание
Анализ переходных процессов – это анализ динамического поведения системы в условиях неустановившегося колебательного процесса. При этом внешняя нагрузка является функцией по времени и известна в любой точке временного интервала ее действия.
При проведении анализа переходных процессов с помощью решателя NX Nastran возможно использование двух методов:
прямого интегрирования уравнения движения – Direct Transient Response (SEDTRAN SOL109)
модального метода (метода суперпозиции форм колебаний) –Modal Transient Response анализ (SEMTRAN SOL112).
Выбор метода зависит от размерности исследуемой системы, необходимой точности результатов, необходимости анализа в высокочастотной области и т.п.
Сравнение результатов расчета прямым и модальным методами частотного анализа
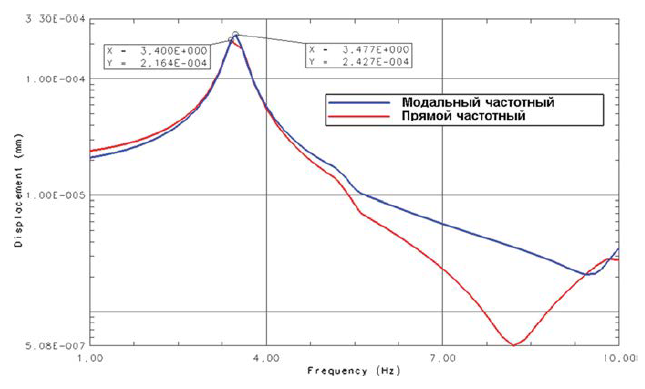
Прямой метод
Основное отличие переходного анализа методом прямого интегрирования системы уравнений движения от частотного анализа заключается в том, что отклик конструкции определяется в отдельных точках временного интервала в соответствии с шагом интегрирования по времени Δt. То есть прямой переходный анализ сводится к решению системы линейных дифференциальных уравнений второго порядка.
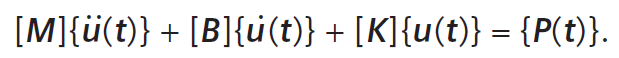
Решение для каждой последующей точки временного интервала t + Δt находится с учетом
решения на предыдущем шаге t.
Линейный анализ переходных процессов подразумевает постоянство во времени матриц [M], [B], [K]. Решение переходного анализа получается путем декомпозиции динамической матрицы. Если в процессе решения шаг интегрирования Δt постоянен, то декомпозиция матрицы осуществляется один раз. На каждом последующем временном шаге происходит только подстановка нового вектора нагрузок, что значительно сокращает вычислительные затраты в случае решения задачи большой размерности. Очевидно, что общее время вычислительного процесса прямо пропорционально количеству шагов интегрирования.
Выбор шага интегрирования
Шаг интегрирования по времени должен иметь достаточную величину для корректного описания изменения нагрузки по времени и поведения системы на максимальной интересующей собственной частоте.
Рекомендуется использовать как минимум десять шагов решения на период отклика на интересующей собственной частоте.
Демпфирование
Структурное демпфирование не может быть задано явно при решении переходного анализа, поэтому требуется его преобразование в эквивалентное вязкое демпфирование. Матрица демпфирования [B] включает несколько компонент:
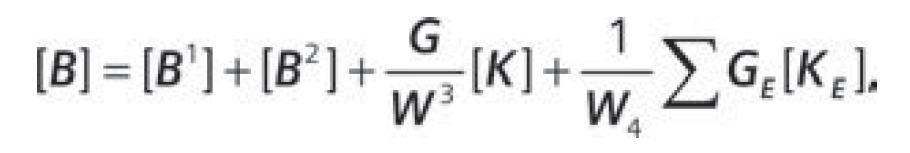
где [B] – матрица, характеризующая вязкое демпфирование отдельных типов конечных элементов CVISC, CDAMPi, CBUSH, CELASi;
G – общий коэффициент конструкционного демпфирования, задаваемый параметром PARAM, G;
W3 – частота преобразования структурного демпфирования в эквивалентное вязкое, задаваемая параметром PARAM, W3, r;
[K] – глобальная матрица жесткости;
[KE] – матрица жесткости элементов;
GE – коэффициент структурного демпфирования элементов, задаваемый при определении свойств материала (GE);
W4 – частота преобразования структурного демпфирования элементов в эквивалентное вязкое, задаваемая параметром PARAM, W4, r.
Пример с использованием прямого метода
В этом исследовании динамического анализа мы рассмотрим прямой метод анализа переходных процессов. Анализ Direct Transient Response можно использовать для определения реакции конструкции на временном промежутке, когда все приложенные нагрузки известны как функции по времени. Во многих случаях желаемыми результатами такого анализа являются узловые перемещения и ускорения, а также силы и напряжения в элементах.
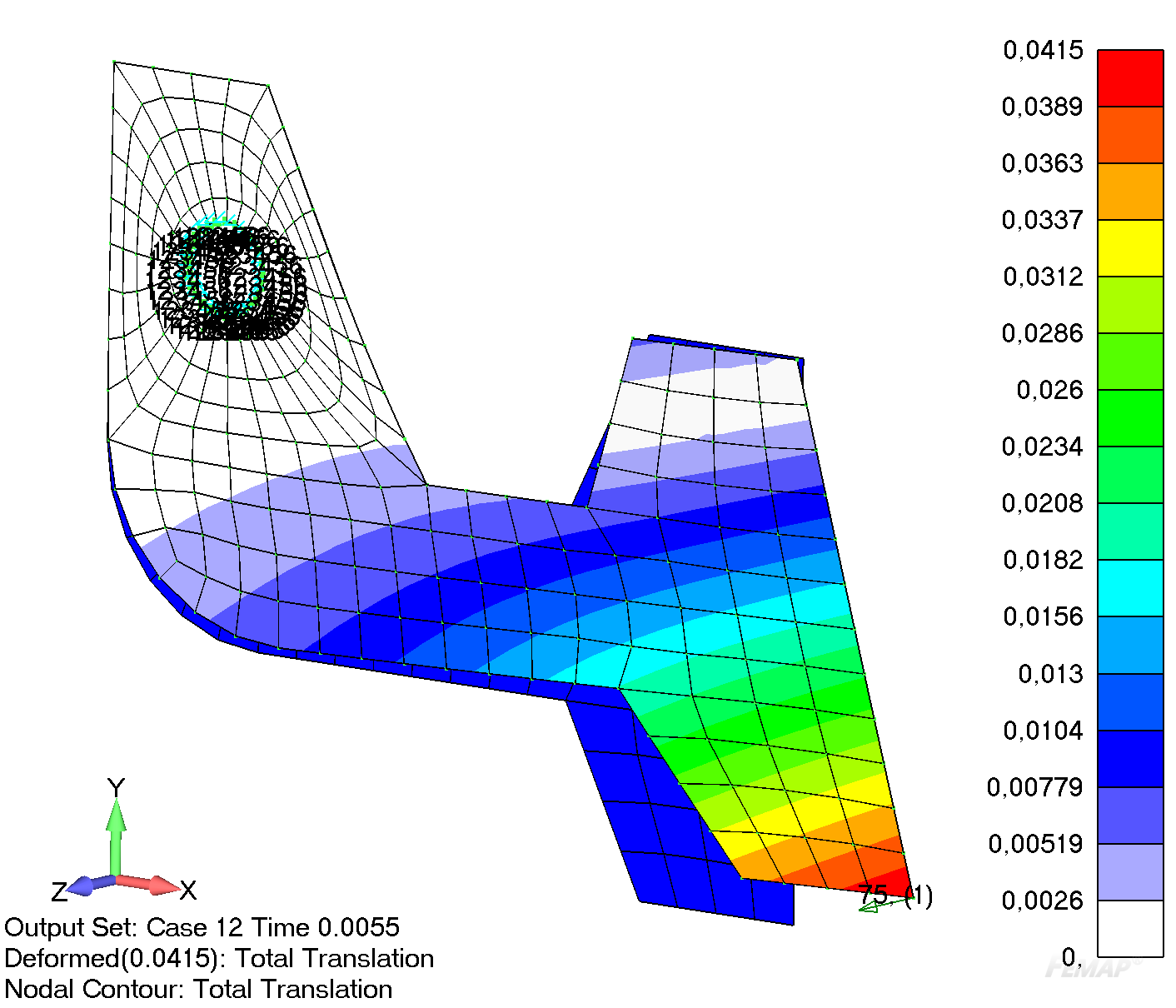
В примере используется модель шарнирного кронштейна и описаны следующие стадии выполнения расчета, который включает в себя:
Создание временной функции нагружения в виде синусоиды
Применение нагрузок и ограничений
Анализ модели решателем NX Nastran
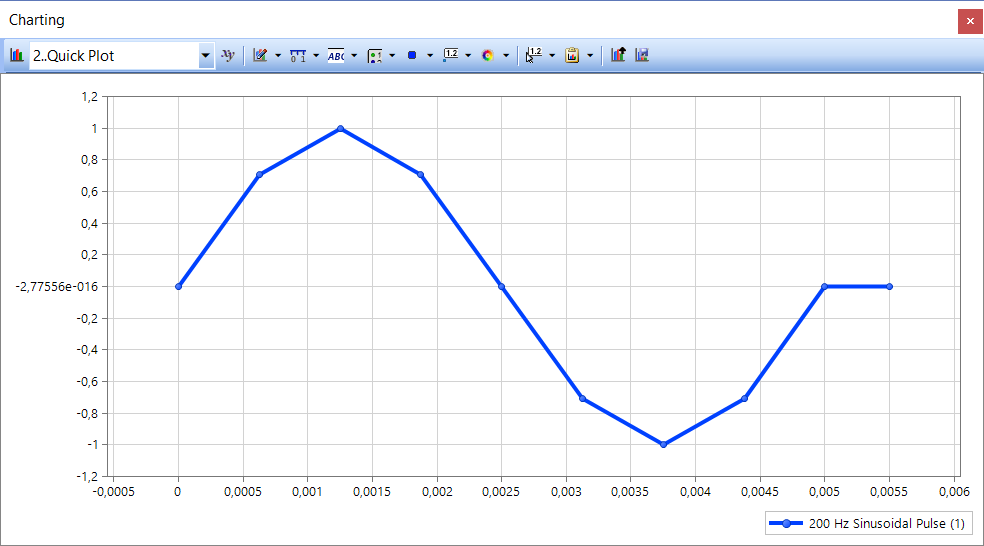
Обработка результатов с помощью построения графиков Charting
Создание функции динамической нагрузки
Чтобы нагрузка зависела от времени, необходимо создать функцию, представляющую из себя синусоидальный импульс.
1. Model, Function.
2. В диалоговом окне Function Definition в поле Title введите название функции «200 Hz sinusoidal pulse».
3. В выпадающем списке Type выберите тип функции, зависящей от времени «1..vs. Time».
4. В разделе Data Entry активируйте режим Equation.
5. Введите следующие значения в соответствующие поля:
X = 0.0
To X = 0.005
Delta X = (0.005/8)
Y = sin(360*200*!x)
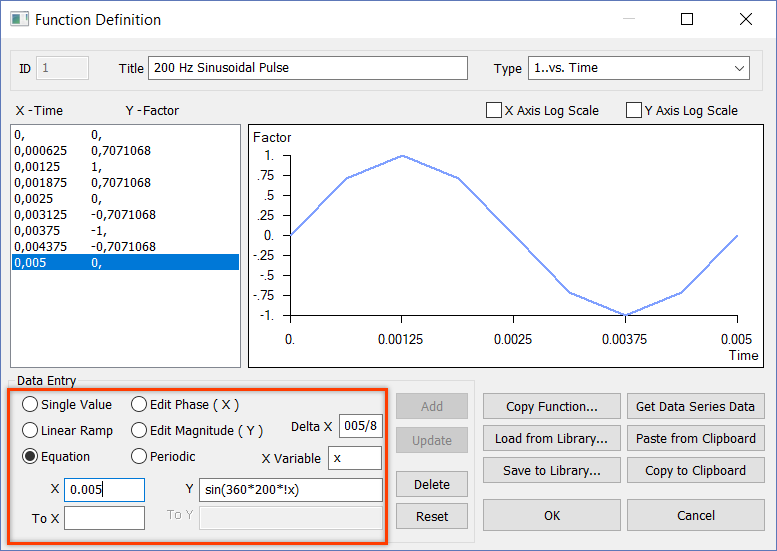
В уравнении Y, используется синтаксис создания формул, который может читать FEMAP. Например, часть уравнения «sin» говорит FEMAP взять синус значения, которое находится в скобках (). Символ «!x» представляет из себя значение переменной «x», поскольку «x» увеличивается от 0.0 до 0.005 с шагом Delta X, равного 0.005/8 (0.000625) для этого примера, который даст нам необходимые 8 точек для создания синусоиды. Значение «200» - частота в Гц.
6. Нажмите кнопку Add, чтобы добавить значения функции. Необходимо обнулить кривую нагрузки после одного импульса, поэтому необходимо добавить одну точку с нулевым значением Y и значением X больше 0.005.
NX Nastran будет использовать координаты кривой для экстраполяции, поэтому необходимо добавить нулевую точку.
7. Переключитесь на режим добавления данных графика «Single Value» и введите следующие значения в соответствующие поля: X =0.0055, Y = 0.00. Нажмите кнопку Add.
Создание изменяющейся во времени нагрузки
1. Приложение переходной нагрузки к кронштейну.
2. Model, Load, Nodal. Поскольку в модели отсутствуют наборы нагрузки, FEMAP предложит создать их.
3. В диалоговом окне New Load Set в поле Title введите название набора «Transient Excitation» и нажмите ОК.
4. В диалоговом окне Entity Selection – Enter Node(s) to Select выберите узел 44 в правом нижнем углу конструкции и нажмите ОК.
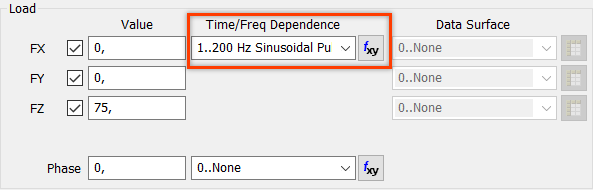
5. В диалоговом окне Create Loads on Nodes выберите силу Force из списка.
6. Введите значение «75» в поле FZ.
7. Выберите «1..200 Hz Sinusoidal Pulse» в выпадающем списке меню функциональных зависимостей.
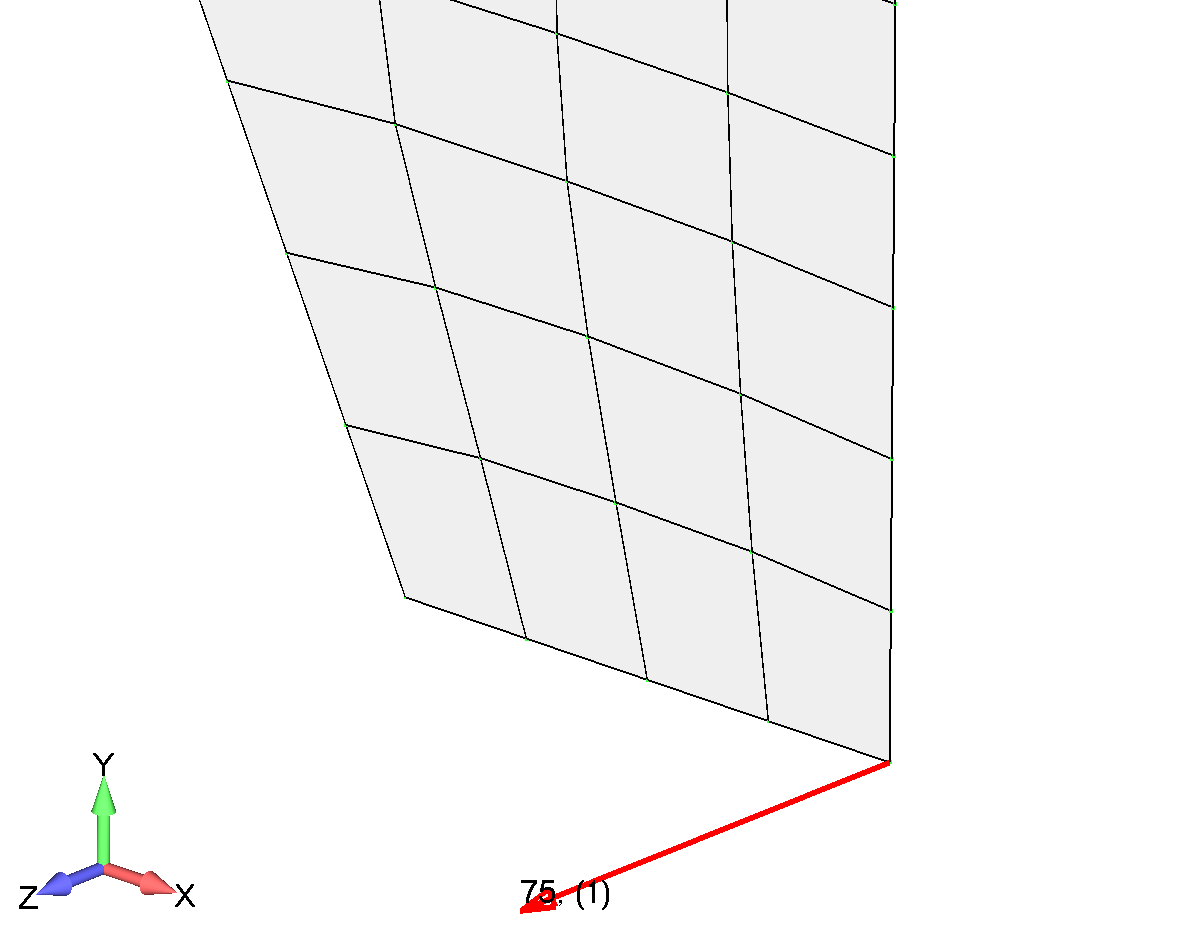
Создание закреплений
Для успешного выполнения анализа, модель должна быть закреплена.
1. Model, Constraint, Nodal.
2. Поскольку в модели не существует наборов ограничений, FEMAP предложит создать их.
3. В диалоговом окне New Constraint Set введите название набора закреплений в поле Title: Hole Fixed. Нажмите ОК.
4. В диалоговом окне Entity Selection – Enter Node(s) to Select Выберите узлы вокруг края отверстия. Это можно сделать, выбирая узлы последовательно, или удерживая клавишу Ctrl щелкнуть рядом с центром окружности и с помощью мыши создать окружность выбора. После того, как все узлы будут находиться внутри кругового окна выбора отпустите кнопку мыши и все узлы будут выбраны.
Удерживая клавишу Shift, можно создать прямоугольную область выбора. Другие варианты, такие как многоугольник и произвольная область выбора доступны по нажатию кнопки Pick в любом диалоговом окне выбора объекта.
5. Нажмите ОК, затем в диалоговом окне Create Nodal Constraints/DOF нажмите кнопку Fixed и нажмите ОК.
6. В диалоговом окне Entity Selection – Enter Node(s) to Select нажмите Cancel.
Настройки анализа
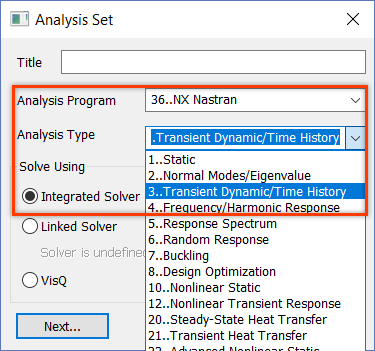
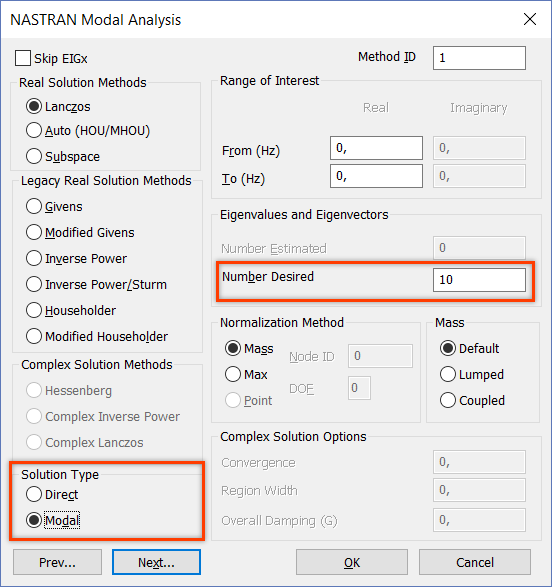
Создайте новый анализ типа 3..Transient Dynamic/Time History и в настройках NASTRAN Modal Analysis в разделе Solution
Type выберите Direct – метод прямого интегрирования уравнения движения.
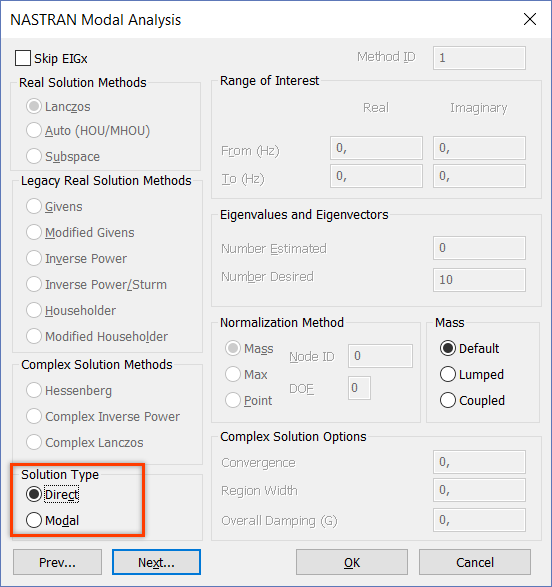
Задайте демпфирование системы и шаг по времени.
- Шаг интегрирования по времени должен иметь достаточную величину для корректного описания изменения нагрузки по времени и поведения системы на максимальной интересующей собственной частоте.
- Рекомендуется использовать как минимум десять шагов решения на период отклика на интересующей собственной частоте.
- Обычно в качестве частоты преобразования W3 используется первая собственная частота свободных колебаний конструкции.
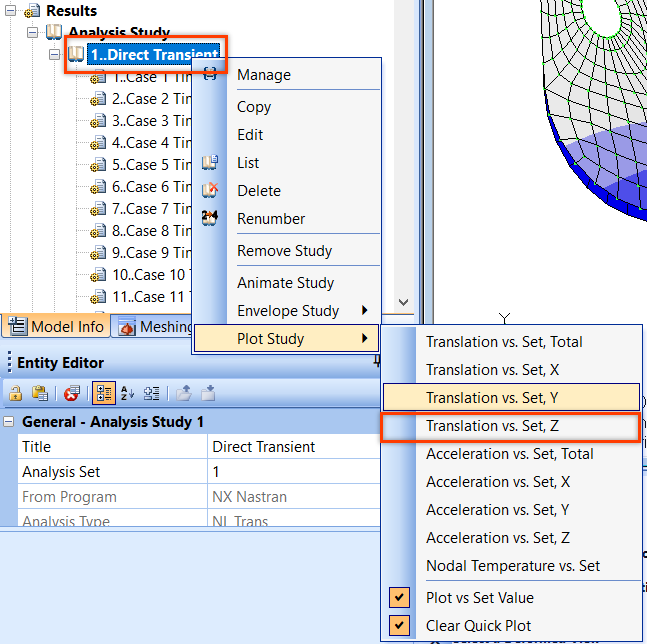
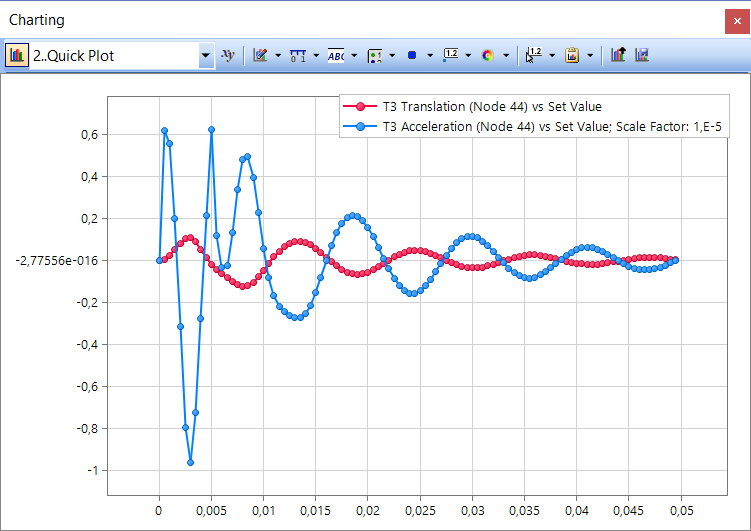
Для быстрого построения графика зависимости перемещений/ускорений от времени нажмите правой кнопкой на набор выходных результатов в дереве проекта Model Info в разделе Results и выберите команду Plot Study.
Модальный метод
При решении задачи большой размерности с целью сокращения вычислительных затрат используется модальный метод для анализа переходных процессов, в основе которого применяется переход от физических координат к модальным.
При использовании модального метода для переходного анализа матрица демпфирования
[B] и глобальная матрица жесткости не являются диагональными, что ведет к невыполнению
условия независимости модальных уравнений движения друг от друга.
Эта проблема решается посредством использования подхода модального демпфирования, подробно описанного выше.
Уравнение движения для i-й собственной формы имеет вид:
При этом в соответствии с уравнением полная реакция системы есть суперпозиция ее реакций по всем учитываемым собственным формам колебаний.
При решении задачи большой размерности с целью сокращения вычислительных затрат используется модальный метод для анализа переходных процессов, в основе которого применяется переход от физических координат к модальным.
При использовании модального метода для переходного анализа матрица демпфирования
[B] и глобальная матрица жесткости не являются диагональными, что ведет к невыполнению
условия независимости модальных уравнений движения друг от друга.
Эта проблема решается посредством использования подхода модального демпфирования, подробно описанного выше.
Уравнение движения для i-й собственной формы имеет вид:
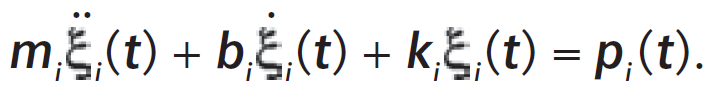
При этом в соответствии с уравнением полная реакция системы есть суперпозиция ее реакций по всем учитываемым собственным формам колебаний.
Рекомендации по выбору метода
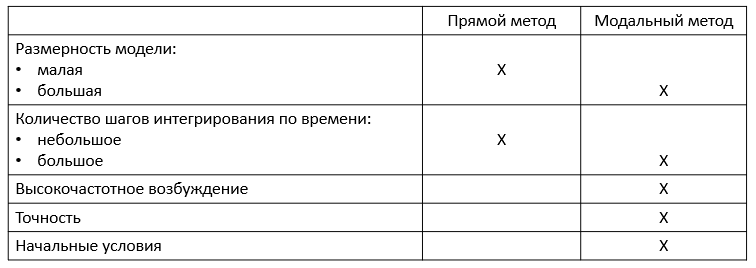
Рекомендации при выборе метода переходного анализа
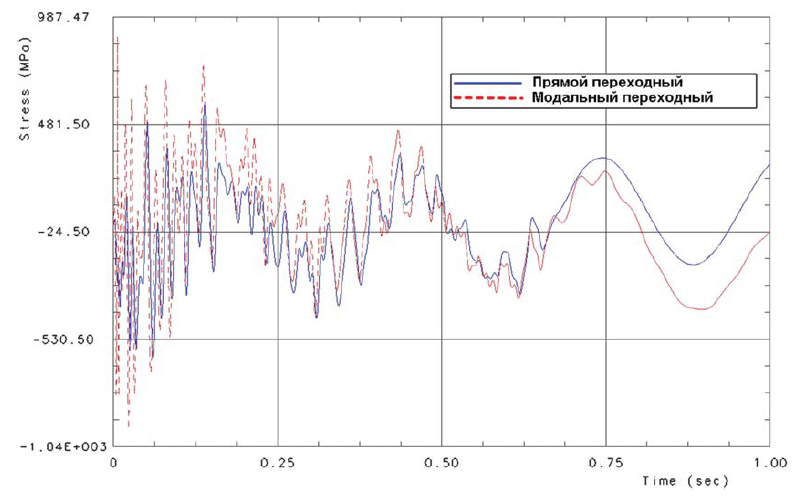
Результаты расчета прямым и модальным методами переходного анализа
Пример с использованием модального метода
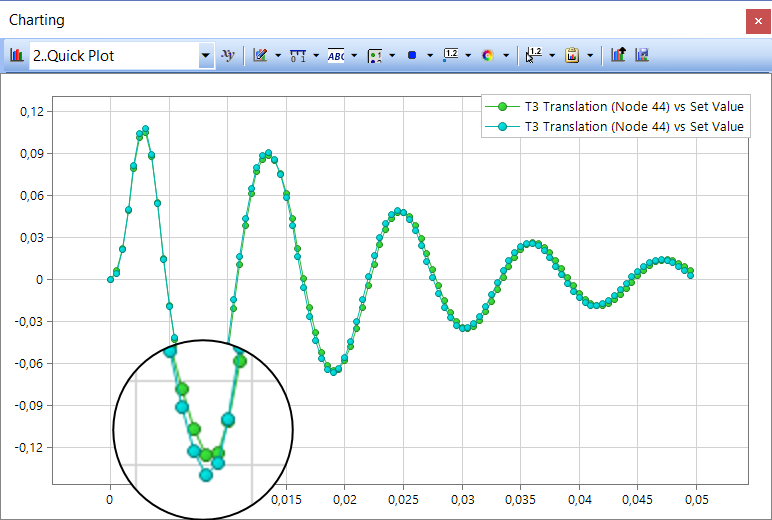
При правильном выборе собственных форм и частот в данной задаче получается практически идеальное совпадение результатов решения задачи модальным методом с методом прямого интегрирования.
Использование модального метода
Если же в анализе модальным методом не учитывать первую форму колебаний кронштейна (собственная частота около 90 Герц), при том, что данная форма является доминирующей и имеет наибольшую эффективную массу в направлении действия импульса, то результаты анализа будут абсолютно неверны.
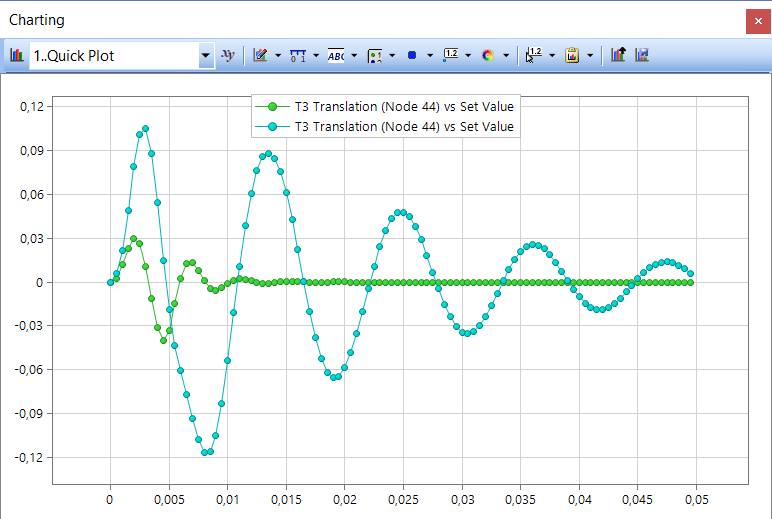
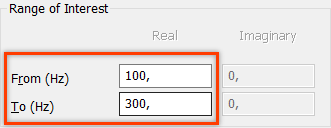
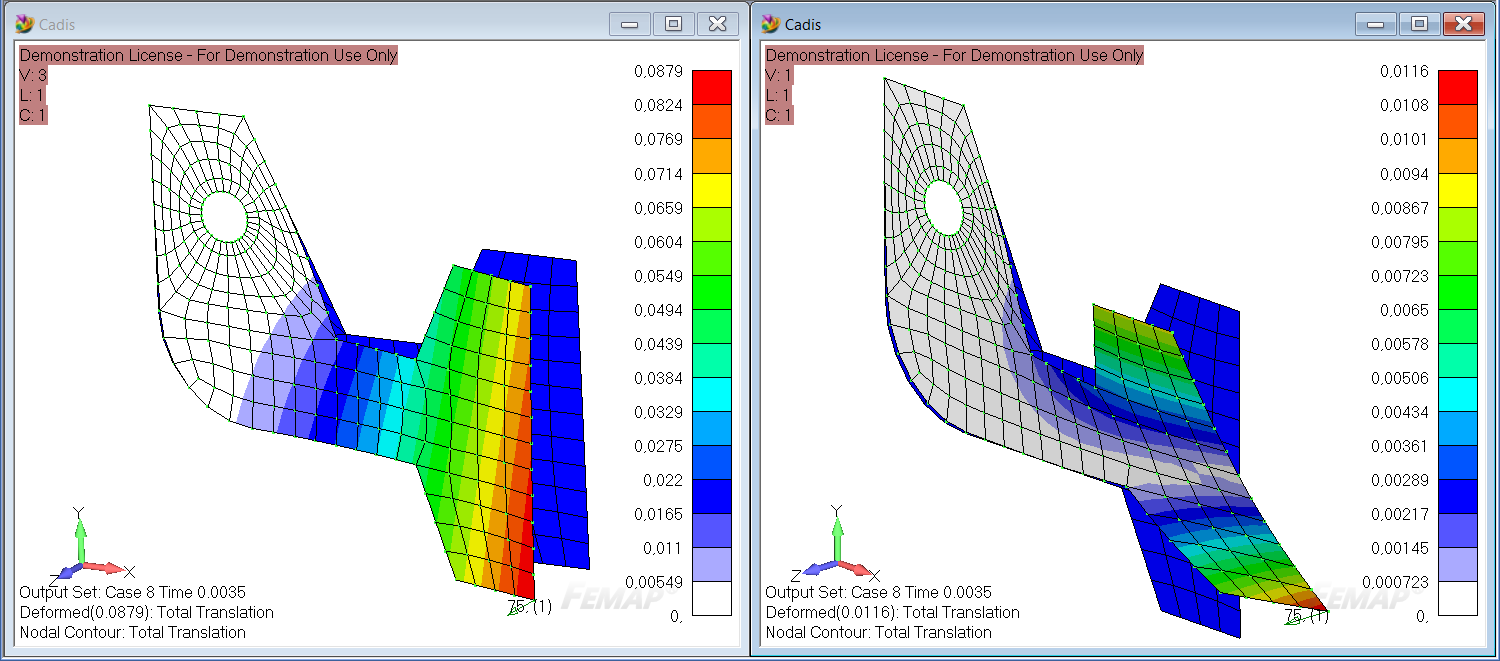
Дополнительные возможности
Во многих ситуациях допустимо рассматривать линейное поведение конструкции в предположении малых
перемещений и деформаций. Однако в некоторых случаях недостаточно учитывать только линейные свойства анализируемой системы, необходимо проводить расчет нелинейными методами. Стоит отметить, что решение нелинейных динамических задач применимо только к анализу неустановившихся колебаний (переходных процессов).
Нелинейность конструкций можно разделить на три категории:
- нелинейность свойств материала;
- геометрическая нелинейность, включающая большие перемещения, большие деформации, изменения вектора нагрузок как функции перемещения конструкции (эффект следящей нагрузки);
- контактное взаимодействие конструкций, зависящее от деформированного состояния.
В том случае, если необходимо учесть нелинейные свойства материала конструкции и/или геометрическую нелинейность (большие перемещения), рекомендуется использовать решения NX Nastran NLTRAN 129 (нелинейный динамический анализ переходных процессов) и NLSTATIC 106 (нелинейный статический анализ).
При решении динамических задач с учетом контактного взаимодействия частей конструкции и/или больших деформаций необходимо использовать решения NX Nastran ADVNL 601, 129 (расширенный нелинейный динамический анализ переходных процессов) и ADVNL 701 (явный расширенный нелинейный динамический анализ).





.svg)






























.jpg)
.jpg)



