Важнейшими составляющими оценки надежности конструкции являются анализ нагрузок, действующих на систему, и расчет ее прочности под воздействием данных нагрузок.
В настоящее время существует два основных подхода к определению нагрузок и прочности: детерминистический и вероятностный.
Детерминистический подход подразумевает, что внешние силы, действующие на систему, могут быть однозначно определены как функции времени или частоты. Соответственно, возможно рассчитать реакцию системы (внутренние нагрузки и напряжения) в любой период эксплуатации системы.
При вероятностном подходе принимается, что известна лишь вероятность того, что сила, действующая на систему, примет то или иное значение в каком-то промежутке времени или частотном диапазоне. В этом случае возможно определить только вероятность достижения параметром системы определенного значения.
Используя детерминистический подход, можно гарантировать надежность конструкции, а при вероятностном можно говорить о надежности конструкции только с определенной вероятностью.
Казалось бы, первый подход предпочтителен, однако, строго говоря при эксплуатации реальных систем очень редко можно однозначно определить внешнее воздействие, поэтому второй подход более универсален.
В настоящее время вероятностные методы анализа прочности и нагрузок широко применяются в авиакосмической (расчеты вибрационной и акустической прочности), автомобильной промышленности (определение воздействия профиля дороги и задачи акустики), при строительстве зданий и сооружений в сейсмоопасных районах и во многих других областях техники.
Цель этого пособия – помочь инженеру научиться в полном объеме использовать этот программный продукт Simcenter Femap в повседневной работе и избежать возможных ошибок.
В первом разделе кратко изложены основы теории случайных процессов.
Второй раздел посвящен описанию алгоритма работы программного обеспечения и рекомендациям
по его применению.
В третьем разделе представлен пример практического применения Simcenter Femap для расчета усталостной прочности обтекателя под действием случайных нагрузок.
Основные соотношения теории случайных процессов
В этом разделе даны основные соотношения теории случайных процессов в объеме, необходимом для правильного понимания работы Simcenter Nastran при анализе на ШСВ.
Случайные процессы описываются при помощи статистических характеристик – интегральных величин, отражающих свойства всей совокупности реализаций данного процесса. Важно отметить, что Simcenter Nastran работает со случайными процессами, удовлетворяющими условиям стационарности и эргодичности.
Стационарным называется случайный процесс, статистические свойства которого не зависят от времени. Примером стационарного случайного процесса могут служить вибрации в двигателе самолета во время полета в крейсерском режиме.
Стационарный случайный процесс является эргодическим, если его статистические характеристики могут быть вычислены осреднением по времени.
Иначе говоря, по одному эргодическому процессу мы можем судить о всем наборе случайных процессов с той же достоверностью, что и по нескольким процессам.
Таким образом, для стационарного эргодического процесса можно определить среднее значение как:

Для описания статистической связи (корреляции) между случайными процессами , в разные моменты времени используются корреляционные функции (автокорреляционные функции):

Если два случайных процесса статистически независимы, то их взаимная корреляционная функция тождественно равна нулю.
Как и обычные функции времени, случайные процессы иногда бывает удобнее анализировать в частотной области. Корреляционная функция и взаимная корреляционная функция могут быть представлены интегралами Фурье:

тогда обратные преобразования Фурье дадут спектральную плотность процессов:

Произведение Sxx (ω) d ω соответствует той доле мощности, которая заключена в интервале частот от ω до ω+d ω. Поэтому функция Sxx (ω) называется иногда спектральной мощностью или спектральной плотностью энергии.
Поскольку спектральные плотности случайных процессов могут быть сравнительно легко найдены экспериментально они получили широчайшее использование в инженерных расчетах.
Одним из таких приложений является анализ линейных систем под действием случайных нагрузок.
Предположим, что на линейную систему действует случайная сила P(t), имеющая спектральную плотность Sp(ω). Передаточная функция системы равна H(ω) (передаточной функцией системы на частоте ω называется отклик системы на синусоидальное воздействие с единичной амплитудой и частотой ω).
Тогда спектральная плотность выходного процесса имеет вид:

Таким образом, зная спектральные плотности входного воздействия, и вычисляя передаточные функции системы, можно по формуле определить спектральную плотность выхода, а зная ее вычислить средний квадрат выходного процесса.
Однако, для большинства задач прочности одного среднего квадрата недостаточно.
Например, для задач усталости необходимо определение количества превышений процессом некоторого порогового значения за единицу времени.
Для этого необходимо знать эффективную частоту или эффективный период случайного процесса. Эти величины могут быть вычислены по формулам:

Реализация анализа случайных процессов в Simcenter Nastran
В Simcenter Nastran случайный анализ включает в себя три основных этапа.
- На первом этапе задается внешнее воздействие и с помощью Nastran определяются комплексные передаточные функции системы.
- На втором этапе задаются спектральные плотности внешнего воздействия и с помощью передаточных функций, полученных на первом этапе, определяются спектральные плотности (Power Spectral Densities PSD) и среднеквадратичные отклонения (Root Mean Square RMS) выходных параметров.
- На третьем этапе осуществляется визуализация результатов (отображение среднеквадратичных сил, напряжений и др. в Femap; отрисовка графиков спектральных плотностей).
Задание внешнего воздействия
При анализе конструкции под воздействием случайных нагрузок первым шагом является задание внешнего воздействия и расчет комплексных передаточных функций.
Этот расчет выполняется в NASTRAN.
Как правило, в инженерных расчетах встречаются три основных типа случайных нагрузок.
- Кинематические случайные нагрузки (обычно это случайные ускорения основания, на котором закреплена конструкция). Если случайная нагрузка является ускорением основания, то этом случае для задания кинематического возбуждения будет использован метод больших масс. То есть в узел конечно-элементной модели, будет помещена большая масса и к этой массе будет приложена сила, величина которой выбирается из расчета получения единичного ускорения в заданном направлении.
- Случайные силы, действующие на различные узлы конструкции.
- Акустические нагрузки, связанные со случайным изменением звукового давления.
Иногда требуется вычислить кинематический отклик от скоростей или перемещений. Для этого также может быть использован метод больших масс. Но функция зависимости силы от частоты (карта TABLED1) должна иметь другой вид:

Применение гравитационных нагрузок (карта GRAV) для моделирования случайного ускорения приводит к существенному увеличению затрат времени и дискового пространства при расчете комплексных переходных функций. Это связано с особенностями алгоритмов программного комплекса Nastran.
В заключение этого раздела следует сказать несколько слов о системах единиц.
Зачастую случайные нагрузки (особенно перегрузки) задаются в единицах g (ускорения свободного падения), а единицы измерения массы и сил численно совпадают.
Во избежание ошибок и для удобства использования в Simcenter Nastran введены два коэффициента:
- на входное воздействие Input (обычно равен g);
- и на матрицу масс WtMass (равен отношению массы к весу, обычно 1/g).
Демпфирование
При любых динамических расчетах сложных систем и, в частности, при расчетах частотного отклика особое внимание следует уделять рассеиванию энергии в конструкции – то есть внутреннему демпфированию.
Как правило, демпфирование определяется из экспериментальных исследований и является функцией частоты и амплитуды колебаний.
В NASTRAN реализована упрощенная модель задания демпфирования в табличном виде с помощью карты TABDMP1 как функция коэффициента усиления Q, доли критического демпфирования CRIT или параметра G, от частоты возбуждения.
Существует взаимнооднозначная связь между этими параметрами:

Нахождение частотного отклика
В Simcenter Nastran для определения частотного отклика (комплексных передаточных функций) может быть использован Frequency Response Analysis прямой или модальный методы (SOL 108, 111 соответственно).
При проведении случайного анализа модальный метод имеет ряд преимуществ.
Во-первых, модальный метод позволяет автоматически вычислять отклик (передаточную функцию) системы при частотах возбуждения равных собственным частотам конструкции. Это чрезвычайно важно, поскольку именно на этих частотах передаточная функция принимает максимальные значения.
И, во-вторых, модальный метод дает возможность задания демпфирования конструкции как функции частоты возбуждения, тогда как прямой метод позволяет задавать только постоянное демпфирование на всех частотах
Однако модальный метод имеет и свои недостатки. В первую очередь они связаны с уменьшением точности расчета. Для правильного использования этого метода необходимо знать его алгоритм.
Задача о нахождении отклика линейных систем на гармоническое воздействие методом конечных элементов сводится к решению системы линейных уравнений:

Решение системы модальным методом происходит в два этапа. На первом этапе решается задача о нахождении собственных частот ω и собственных векторов ϕ системы c нулевой правой частью.
Если в решении учтены все собственные тона колебаний системы, то оно является точным. На практике приходится учитывать только часть тонов, лежащих вблизи диапазона частот возбуждения.
Чем больше собственных тонов учтено, тем точнее решение.
Ширина частотного диапазона, в котором должны быть найдены все тона колебаний системы, определяется исходя из свойств конкретной системы на основании инженерного опыта.
Обычно бывает достаточно найти все низшие тона до частоты в 1.5 раза превышающей наивысшую частоту возбуждения
Другим параметрами, влияющими на точность определения передаточных функций, являются число и плотность задания точек по частоте, в которых должен вычисляться отклик.
В Simcenter Femap они могут быть заданы с помощью карт:
- FREQ – непосредственное задание списка частот;
- FREQ1 – задание нижней частоты, приращения и количества приращений;
- FREQ2 – задание границ диапазона и количества частот внутри него;
- FREQ3 – задание границ диапазона и количества частот между соседними собственными частотами внутри диапазона;
- FREQ4 – задание относительной ширины диапазона частот вокруг собственных частот и количества точек внутри него;
- FREQ5 – задание частот, как долей от собственных.
В Simcenter Femap поддерживаются все способы задания частот отклика.
Можно комбинировать различные способы в зависимости от конкретной задачи. Однако, необходимо задание одной из карт FREQ3, FREQ4 или FREQ5 для того, чтобы NASTRAN вычислял отклик на собственных частотах системы.
Очевидно, что чем больше будет задано точек по частоте, тем полнее будет определена передаточная функция.
Не следует злоупотреблять и задавать слишком много точек отклика, поскольку это может привести к существенному увеличению затрат времени и ресурсов при расчете.
Удаление «ненужных» собственных форм
Существуют несколько путей удаления из расчета «ненужных» форм:
1. Наиболее простой путь - использование Bulk Data параметров.
PARAM,LFREQ - при выполнении модального решения будут игнорированы все собственные формы, соответствующая частота колебаний которых меньшие чем значение LFREQ (Гц);
PARAM,HFREQ - при выполнении модального решения будут игнорированы все собственные формы, соответствующая частота колебаний которых превышает значение HFREQ (Гц);
PARAM,LMODES - определяет число форм, начиная с первой, чья соответствующая частота колебаний превышает значение LFREQ, которые будут учтены в данном динамическом решении.
Как видим, недостаток такого подхода - его недостаточная гибкость. Формы удаляются целыми диапазонами. Что не всегда удобно.

2. Использование суперэлементов - позволяет пользователю удалять ненужные формы по соответствующим компонентам или по сборкам
3. Использование DMAP - позволяет пользователю удалить из расчета конкретный список ненужных форм. Данный alter может быть использован в любом модальном динамическом решении (SOL 103, 110, 111, 112...)
Расчет отклика на случайное воздействие
Случайный анализ в Simcenter Femap сводится либо к вычислению среднеквадратичных значений (RMS) для всех параметров, для которых были предварительно определены комплексные передаточные функции, либо к расчету спектральной плотности (PSDF), кумулятивного среднеквадратичного значения (CRMS) или автокорреляционной функции для выбранного параметра одного или нескольких узлов или элементов модели.
При проведении случайного анализа следует обратить внимание на то, в каком масштабе заданы спектральные плотности внешних воздействий (линейном или логарифмическом). Несоответствие масштаба может вызвать неточность вычислений.
После задания случайного входа, если используется меню RMS Analysis, будет произведен расчет среднеквадратичных значений (RMS) для всех параметров модели, для которых имеются передаточные функции.
Кумулятивное среднеквадратичное значение (CRMS) вычисляется по формуле:

Наиболее очевидным способом определения статистических характеристик напряжений является расчет, при котором случайная нагрузка непосредственно прикладывается к подробной модели всей конструкции. При этом обеспечивается наибольшая точность и достоверность расчета.
В реальных условиях работы КБ, как правило, не имеет смысла (или даже невозможно) использовать подробную динамическую модель всей конструкции для расчета прочности каждой отдельной детали. Поэтому применяется подход при котором динамический расчет всей конструкции по упрощенной модели выполняет отдел нагрузок, а прочнист использует эти результаты в качестве исходных данных.
В качестве нагрузок для статического анализа сабмодели можно взять среднеквадратичные значения (RMS) усилий по границе. Поскольку RMS величина всегда положительная, она дает представление только об абсолютном значении нагрузки. Поэтому для получения консервативного результата необходимо выбрать наихудшую комбинацию нагрузок с учетом их направления (+ или -).
Такая оценка случайных напряжений является наиболее распространенной. Она наиболее проста и наглядна, требует минимальных затрат машинных ресурсов. Однако она является очень консервативной.
Для уменьшения степени консервативности расчета напряжений вместо статического анализа может быть применен случайный анализ, а в качестве нагрузок взяты не RMS продольных сил и перегрузки, а их спектральные и взаимные спектральные плотности, вычисленные по формулам:

В этом случае статистические характеристики напряжений не должны отличаться от полученных из расчета по полной модели.
Заключение
В данном методическом пособии показаны возможности программного продукта Simcenter Femap и способы его применения для расчета конструкций на ШСВ.
Для корректного использования методики в инженерных расчетах необходимо остановиться на некоторых особенностях программного обеспечения и описанных методов анализа:
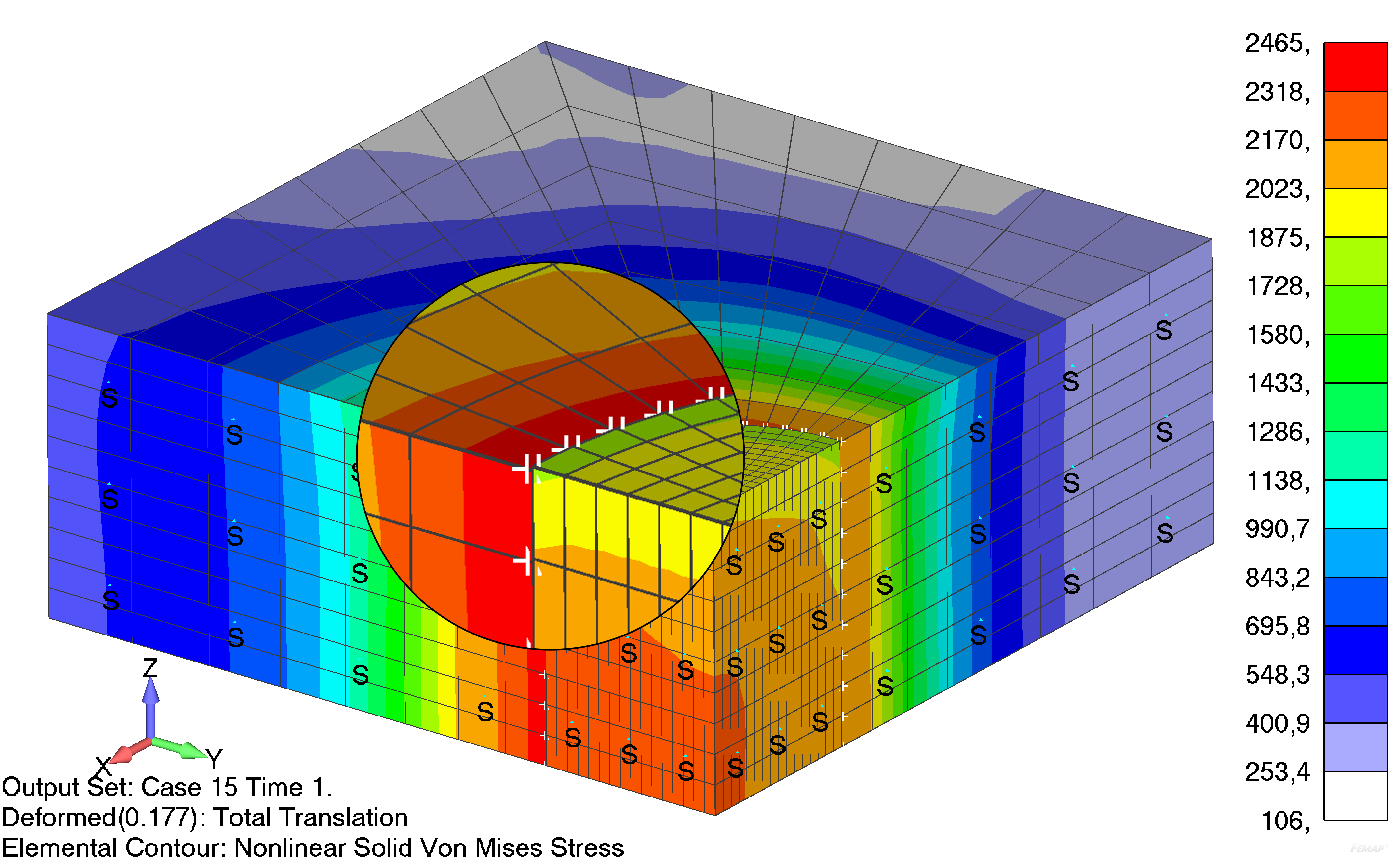
1. При анализе среднеквадратичных напряжений по фон-Мизесу или по главным напряжениям следует иметь в виду, что Femap вычисляет эти характеристики как функцию от среднеквадратичных значений компонент тензора напряжений, что вносит дополнительный консерватизм в их оценку. Для более точного определения среднеквадратичных значений этих характеристик тензора напряжений надо, вообще говоря, вычислять для них комплексные передаточные функции, что не предусмотрено. Для этого может быть использовано другое программное обеспечение.
Пошаговое руководство анализа на ШСВ
В Simcenter Nastran случайный анализ включает в себя три основных этапа:
1. На первом этапе задается внешнее воздействие и с помощью Nastran определяются комплексные передаточные функции системы.
2. На втором этапе задаются спектральные плотности внешнего воздействия и с помощью передаточных функций, полученных на первом этапе, определяются спектральные плотности (Power Spectral Densities PSD) и среднеквадратичные отклонения (Root Mean Square RMS) выходных параметров.
3. На третьем этапе осуществляется визуализация результатов (отображение среднеквадратичных сил, напряжений и др. в Femap; отрисовка графиков спектральных плотностей).
Создание нагрузочной функции
Сперва нужно создать функцию для нагрузки. Это простая функция которая определяет постоянную нагрузку во всем частотном диапазоне.
Координаты функции (1;1) и (1;10000)

Создание функции демпфирования
Если демпфирование конструкции зависит от частоты то его также можно задать в виде функции
Доступны три типа функции демпфирования:
6..Structural Damp vs. Freq – задание коэффициента структурного демпфирования G=2*ζ
7..Critical Damp vs. Freq – задание функции критического демпфирования ζ
8..Q Damping vs. Freq – зависимость добротности Q от частоты. Q = 1/(2*ζ)
где ζ – коэффициент критического демпфирования

- Далее необходимо создать PSD функцию по известным значениям ускорения
- Амплитуда PSD функции вводится в g^2/Гц
- Для того чтобы получить результаты ускорений в см/с^2, нагрузка позже будет отмасштабирована
Создание узла для приложения ускорений
- Создаем в центре узел и соединяем его с основной моделью с помощью RBE2 элемента

Приложение нагрузки
- Создаем новый набор нагрузок и прикладываем узловую нагрузку к независимому узлу RBE2 элемента Выбираем тип нагрузки Acceleration
- Задаем амплитуду нагрузки 9,81 м/с^2 – таким образом мы масштабируем нагрузку и результаты будут выводиться не для ускорений в g, а в см/с^2
- Выбираем ранее созданную нагрузочную функцию

Закрепление модели
- Закрепляем узел к которому прикладывалась нагрузка по всем степеням свободы
- Для правильной работы нагрузок типа «вынужденное движение» (перемещение, скорость, ускорение) необходимо закреплять степени свободы по которым прикладывается нагрузка.

Задание групп для вывода результатов
По умолчанию результаты для всей модели не выводятся. Пользователь сам должен выбрать интересующие узлы и элементы. Для этого нужно создать группу в которую нужно добавить узлы и элементы для которых будут выводиться результаты.
Добавим в группу узел к которому прикладывается нагрузка и несколько узлов на конструкции.


Настройка анализа
- Создаем новый анализ. Выбираем тип 6..Random Response
- В настройках модального анализа NASTRAN Modal Analyses выбираем модальный метод решения Modal и задаем параметры диапазона исследуемых частот
- Найденные в результате модального анализа собственные частоты и формы будут использоваться в определении отклика конструкции методом суперпозиции форм
- Рекомендуется задавать частотный диапазон в два раза больше исследуемого (4000 Гц в данном случае для диапазона 20-2000 Гц) а значение запрашиваемых частот «Number Desired» оставить нулевым, тогда решатель будет искать все частоты в диапазоне без урезания.

В методе нормальных форм большее число частот дает более точный результат. Число форм должно быть достаточно велико, чтобы покрыть интересующий частотный диапазон (термин «интересующий диапазон» означает диапазон частот, чей отклик должен быть вычислен, а также диапазон частот, на которых прикладывается нагрузка). Как общее правило, должно быть достаточно форм для того, чтобы покрыть диапазон вплоть до примерно удвоенной высшей интересующей частоты.
Например, если отклик должен быть вычислен до 100 Гц, то должно быть использовано достаточно форм, в диапазоне, как минимум до 200 Гц.
Как другое общее правило, вы должны использовать достаточно форм, чтобы покрыть диапазон в 2-10 раз больший, чем основная частота отклика.
Сравнение результатов PSDF рефлектора модальным методом при вычислении частот в диапазоне от 0 до 2000 Гц (красный график) и от 0 до 4000 Гц (черный график).

Настройка анализа частотного отклика
- В окне Dynamic Analysis выбираем ранее созданную таблицу модального демпфирования в пункте Modal Damping Table, если демпфирование постоянно то можно задать только коэффициент структурного демпфирования G, в ячейке выше Overall Structural Damping Coeff (G)
- Раздел Modal Freq позволяет задать частоты для отклика на основе посчитанных ранее собственных частот по аналогии с FREQ4 – задание относительной ширины диапазона частот вокруг собственных частот и количества точек внутри него. Можно запросить несколько частот (обычно 5-7) вокруг резонансной частоты

- На вкладке Solution Frequencies можно задать частоты в виде последовательности.
- FREQ – непосредственное задание списка частот; FREQ1 – задание нижней частоты, приращения и количества приращений; FREQ2 – задание границ диапазона и количества частот внутри него; FREQ3 – задание границ диапазона и количества частот между соседними собственными частотами внутри диапазона; FREQ4 – задание относительной ширины диапазона частот вокруг собственных частот и количества точек внутри него; FREQ5 – задание частот, как долей от собственных.
Можно комбинировать различные способы в зависимости от конкретной задачи. Однако, необходимо задание одной из карт FREQ3, FREQ4 или FREQ5 для того, чтобы NASTRAN вычислял отклик на собственных частотах системы.
- Очевидно, что чем больше будет задано точек по частоте, тем полнее будет определена передаточная функция.
- Не следует злоупотреблять и задавать слишком много точек отклика, поскольку это может привести к существенному увеличению затрат времени и ресурсов при расчете.
FREQ3, FREQ4, FREQ5 вычисляют частоты решения на основе результатов модального анализа. При решении прямым методом Direct точки решения, посчитанные этими способами, вычислены не будут.

Запрос вывода результатов
Анализ случайной вибрации является постпроцессингом анализа частотного отклика (гармонического анализа). По умолчанию результаты частотного отклика будут выводиться вне зависимости от настроек Random Response.
В окне Output for Random Analysis можно выбрать тип результатов, которые будут выводиться (PSD функции, функции автокорреляции, среднеквадратичные значения или все результаты сразу)

- В следующем окне можно выбрать отдельные векторы результатов (ускорения, напряжения)
- В данном случае выбраны только ускорения по направлению Y
- Далее появляются окна выбора групп с узлами и элементами для вывода результатов


Задание PSD функции
В окне Power Spectral Density Factors нужно присвоить ранее созданную PSD функцию к набору нагрузок

Выбор граничных условий
- Граничные условия задаются так же как и для анализа частотного отклика
- Задается набор закреплений и нагрузок

Анализ результатов
- После завершения расчета выводятся такие типы результатов
- X-Y Plot Summary – набор векторов, таких величин как среднеквадратичные амплитуды, пиковые значения и прочие.
- PSDF 1 Freq – выходные PSD функции RMS Values – среднеквадратичные значения амплитуд, соответствуют значению 1σ. Среднеквадратическое значение спектра это одно число, представляющее общий уровень энергии в диапазоне частот. Определяется как кв. корень из площади под графиков PSDF во всем диапазоне частот
- Positive Crossings – Эффективная частота. Используется для расчетов усталости.
- CRMS 1 Freq – кумулятивные среднеквадратичные значения:

Показывает на каких частотах содержится наибольшее число энергии. Позволяет вычислять среднеквадратичные значения RMS в поддиапазонах частот.
Анализ результатов PSDF и RMS Value
На графике приведена выходная функция PSD реакции T2 Constrain Force (ось Y), которая была получена умножением передаточной функции, вычисленной в гармоническом анализе, на входную функцию PSD.
RMS Value T2 Constrain Force во всем диапазоне частот от 0 до 2000 Гц вычисляется как квадратный корень из площади под графиком PSDF.


Анализ результатов CRMS
CRMS (кумулятивное среднеквадратичное значение) вычисляется по формуле:

- Показывает на каких частотах содержится наибольшее число энергии.
- Позволяет вычислять среднеквадратичные значения RMS в поддиапазонах частот.

PARAM, RMSINT
По умолчанию PARAM, RMSINT = LINEAR для трапецеидального приближения.
RMSINT определяет метод интерполяции для численного интегрирования при вычислении RMS (среднеквадратичное значение) и Positive Crossing (число пересечений нуля или эффективная частота) по PSDF (функция спектральной плотности мощности).
- RMSINT = LINEAR запрашивает трапецеидальное приближение, которое является подходом по умолчанию в Simcenter Nastran.
- RMSINT = LOGLOG запрашивает интерполяцию log-log.
Анализ результатов CRMS
Вычисление среднеквадратичного значения RMS в нужном диапазоне частот (например, в диапазоне частот вырезания) графически изображено на следующем слайде.
Есть два способа:
- 1. Посчитать анализ на ШСВ в диапазоне частот вырезания и посмотреть значение RMS Value. Лучше использовать прямой метод Direct, так как для модальный может дать не точные результаты из-за малого количества форм в диапазоне.
- RMS в диапазоне вырезания (freq1; freq2) вычисляется как:
RMS(freq1;freq2)=sqrt(CRMS(freq2)^2-CRMS(freq1)^2)
Второй метод предпочтительнее, так как дает достаточно точные результаты без дополнительных вычислений.
Вычисление RMS в диапазоне частот необходимо для сравнения значения с квазистатической нагрузкой при вырезании входного воздействия PSDF.

Методика вырезания
Цель методики вырезания состоит в том, чтобы уменьшить нереально завышенные реакции, возникающими при резонансах испытательного образца во время вибрационных испытаний до квазистатических нагрузок.
Цель методики вырезания состоит в том, чтобы уменьшить нереально завышенные реакции, возникающими при резонансах испытательного образца во время вибрационных испытаний до квазистатических нагрузок.

1. Критерий непревышения при воздействии по оси X (в КЭ-модели это ось Y):
M x g x 15 = 21,71 x 9,8 x 15 = 3 191,37 Н
2. Это расчетное значение сравнивается с результирующим среднеквадратичным значением (RMS) реакции 3 сигма, рассчитанным в конкретной полосе вырезания:
3х RMS(freq1;freq2)=3х sqrt(CRMS(freq2)^2-CRMS(freq1)^2)
3. Полоса вырезания определяется на основе частот с наибольшей эффективной массой в направлении воздействия. В модели рефлектора первая собственная частота в направлении воздействия 195,4 Гц.
Freq1= 195,4 x (2)^-0,25 = 164,31 Гц
Freq2= 195,4 x (2)^0,25 = 232,37 Гц
Это только один из способов вычисления полосы вырезания, есть альтернативные методы, которые необходимо согласовывать с заказчиком.
Частоты 164,31 и 232,37 Гц нужно добавить в точки решения анализа Random Response с помощью карты FREQ0, либо в таблицу Modal Frequency Table.
4. Вычислим среднее квадратичное значение реакции в направлении воздействия в диапазоне вырезания:
3х RMS(164,31; 232,37)=3х sqrt(CRMS(232,37)^2-CRMS(164,31)^2) = 3х sqrt(5039,46^2-1983,46^2) = 3x 1 983,46 = 5 950,38 Н

5. Среднее квадратичное значение в диапазоне вырезания равно квадратному корню из площади под графиком реакции PSDF в этом же диапазоне. Площадь под графиком Nastran вычисляет разными численными методами, описанными в слайде 46 (PARAM, RMSINT).

6. Среднее квадратичное значение реакции 3 сигма в диапазоне вырезания (5 950,38 Н) не должно превышать уровень квазистатической реакции (3 191,37 Н).
Уменьшим уровень PSDF в диапазоне вырезания в 4 раза. Конечный уровень может определяться итеративным способом.

6. Среднее квадратичное значение реакции в направлении воздействия в диапазоне вырезания с новой входной PSDF (показана на предыдущем слайде):
3х RMS(164,31; 232,37)=3х sqrt(CRMS(232,37)^2-CRMS(164,31)^2) =
3х sqrt(3501,67^2-1983,46^2) = 3x 1 983,46 = 2 885 Н < 3 191,37 Н (критерий по квазистатике)

7. Аналогичная процедура вырезания осуществляется для всех собственных частот с наибольшей эффективной массой в заданном направлении где имеет место быть превышение квазистатических нагрузок.
Диапазон частот вырезания и характер вырезания входной PSDF может осуществляться различными способами по согласованию с заказчиком.





.svg)




























.jpg)
.jpg)



